😎前言

二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。但是，折半查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列。

查找过程：

首先，假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

算法要求：

1.必须采用顺序存储结构。
2.必须按关键字大小有序排列。

比较次数：

计算公式：
当顺序表有n个关键字时：
查找失败时，至少比较a次关键字；
查找成功时，最多比较关键字次数是b。
注意：a,b,n均为正整数。

算法复杂度：

二分查找的基本思想是将n个元素分成大致相等的两部分，取a[n/2]与x做比较，如果x=a[n/2],则找到x,算法中止；如果x<a[n/2],则只要在数组a的左半部分继续搜索x,如果x>a[n/2],则只要在数组a的右半部搜索x.
时间复杂度即是while循环的次数。
总共有n个元素，
渐渐跟下去就是n,n/2,n/4,…n/2^k（接下来操作元素的剩余个数），其中k就是循环的次数
由于你n/2^k取整后>=1
即令n/2^k=1
可得k=log2n,（是以2为底，n的对数）
所以时间复杂度可以表示O(h)=O(log2n)

🌲山脉数组的峰顶索引

🚩题目描述：

符合下列属性的数组 arr 称为 山脉数组 ：
arr.length >= 3
存在 i（0 < i < arr.length - 1）使得：

• arr[0] < arr[1] < … arr[i-1] < arr[i]

• arr[i] > arr[i+1] > … > arr[arr.length - 1]

给你由整数组成的山脉数组 arr ，返回满足 arr[0] < arr[1] < … arr[i - 1] < arr[i] > arr[i + 1] > … > arr[arr.length - 1] 的下标 i 。

你必须设计并实现时间复杂度为 O(log(n)) 的解决方案。

• 示例 1：
  输入：arr = [0,1,0]
  输出：1

• 示例 2：
  输入：arr = [0,2,1,0]
  输出：1

• 示例 3：
  输入：arr = [0,10,5,2]
  输出：1

class Solution {public int peakIndexInMountainArray(int[] arr) {}
}

🚩算法思路

1、分析峰顶位置的数据特点，以及⼭峰两旁的数据的特点：

• 峰顶数据特点： arr[i] > arr[i - 1] && arr[i] > arr[i + 1] ；

• 峰顶左边的数据特点： arr[i] > arr[i - 1] && arr[i] < arr[i + 1] ，也就是呈现上升趋势

• 峰顶右边数据的特点： arr[i] < arr[i - 1] && arr[i] > arr[i + 1] ，也就是呈现下降趋势

2.、因此，根据 mid 位置的信息，我们可以分为下⾯三种情况：

• 如果 mid 位置呈现上升趋势，说明我们接下来要在 [mid + 1, right] 区间继续搜索；

• 如果 mid 位置呈现下降趋势，说明我们接下来要在 [left, mid - 1] 区间搜索；

• 如果 mid 位置就是⼭峰，直接返回结果

🚩代码实现：

class Solution {public int peakIndexInMountainArray(int[] arr) {int left = 1;int right = arr.length - 2;while(left < right) {int mid = left + (right - left + 1) / 2;if(arr[mid] > arr[mid - 1]) {left = mid;} else {right = mid - 1;}}return left;}
}

🌴寻找峰值

🚩题目描述

峰值元素是指其值严格大于左右相邻值的元素。

给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞ 。

你必须实现时间复杂度为 O(log n) 的算法来解决此问题。

• 示例 1：
  输入：nums = [1,2,3,1]
  输出：2
  解释：3 是峰值元素，你的函数应该返回其索引 2。
• 示例 2：
  输入：nums = [1,2,1,3,5,6,4]
  输出：1 或 5
  解释：你的函数可以返回索引 1，其峰值元素为 2；或者返回索引 5， 其峰值元素为 6。

class Solution {public int findPeakElement(int[] nums) {}
}

🚩算法思路：

寻找⼆段性：
任取⼀个点 i ，与下⼀个点 i + 1 ，会有如下两种情况：

1. arr[i] > arr[i + 1] ：此时「左侧区域」⼀定会存在⼭峰（因为最左侧是负⽆穷），那么我们可以去左侧去寻找结果；

2. arr[i] < arr[i + 1] ：此时「右侧区域」⼀定会存在⼭峰（因为最右侧是负⽆穷），那么我们可以去右侧去寻找结果

当我们找到「⼆段性」的时候，就可以尝试⽤「⼆分查找」算法来解决问题

🚩代码实现

class Solution {public int findPeakElement(int[] nums) {int left = 0;int right = nums.length - 1;if(right < 1) {return 0;}while(left < right) {int cmd = (left + right + 1) / 2;if(nums[cmd -1] <= nums[cmd] ) {left = cmd;} else {right = cmd -1;}}return left;}
}

🍀寻找旋转排序数组中的最小值

🚩题目描述

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

• 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
• 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

• 示例 1：
  输入：nums = [3,4,5,1,2]
  输出：1
  解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

• 示例 2：
  输入：nums = [4,5,6,7,0,1,2]
  输出：0
  解释：原数组为 [0,1,2,4,5,6,7] ，旋转 4 次得到输入数组。

• 示例 3：
  输入：nums = [11,13,15,17]
  输出：11
  解释：原数组为 [11,13,15,17] ，旋转 4 次得到输入数组

class Solution {public int findMin(int[] nums) {}
}

🚩算法思路

题⽬中的数组规则如下图所⽰：

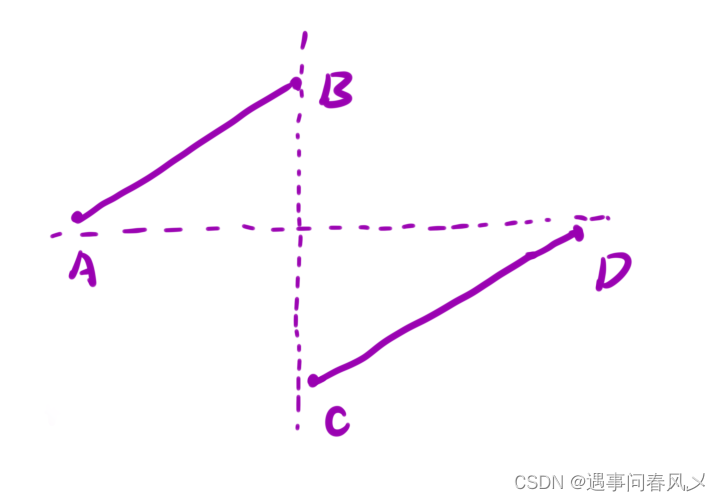
其中 C 点就是我们要求的点。

⼆分的本质：找到⼀个判断标准，使得查找区间能够⼀分为⼆。

通过图像我们可以发现， [A，B] 区间内的点都是严格⼤于 D 点的值的， C 点的值是严格⼩于 D 点的值的。但是当 [C，D] 区间只有⼀个元素的时候， C 点的值是可能等于 D 点的值的。

因此，初始化左右两个指针 left ， right ：

然后根据 mid 的落点，我们可以这样划分下⼀次查询的区间：

• 当 mid 在 [A，B] 区间的时候，也就是 mid 位置的值严格⼤于 D 点的值，下⼀次查询区间在 [mid + 1，right] 上；
• 当 mid 在 [C，D] 区间的时候，也就是 mid 位置的值严格⼩于等于 D 点的值，下次

查询区间在 [left，mid] 上。

当区间⻓度变成 1 的时候，就是我们要找的结果

🚩代码实现

class Solution {public int findMin(int[] nums) {int left = 0;int right = nums.length - 1;int cmp = nums[right];while(left < right) {int cmd = (left + right ) / 2;if(nums[cmd] > cmp) {left = cmd + 1;} else {right = cmd;}}return nums[left];}
}

🎍点名

🚩题目描述

某班级 n 位同学的学号为 0 ~ n-1。点名结果记录于升序数组 records。假定仅有一位同学缺席，请返回他的学号。

• 示例 1:
  输入: records = [0,1,2,3,5]
  输出: 4

• 示例 2:
  输入: records = [0, 1, 2, 3, 4, 5, 6, 8]
  输出: 7

🚩思路解析

关于这道题中，时间复杂度为 O(N) 的解法有很多种，⽽且也是⽐较好想的，这⾥就不再赘述。

本题只讲解⼀个最优的⼆分法，来解决这个问题。
在这个升序的数组中，我们发现：

• 在第⼀个缺失位置的左边，数组内的元素都是与数组的下标相等的；

• 在第⼀个缺失位置的右边，数组内的元素与数组下标是不相等的。

因此，我们可以利⽤这个「⼆段性」，来使⽤「⼆分查找」算法。

🚩代码实现

class Solution {public int missingNumber(int[] nums) {int left = 0;int right = nums.length - 1;while(left < right) {int mid = left + (right - left) / 2;if(nums[mid] == mid) {left = mid + 1;} else {right = mid;}}return left == nums[left] ? left + 1 : left;}
}

⭕总结

关于《【算法优选】 二分查找专题——贰》就讲解到这儿，感谢大家的支持，欢迎各位留言交流以及批评指正，如果文章对您有帮助或者觉得作者写的还不错可以点一下关注，点赞，收藏支持一下！