深入理解强化学习——序列决策（Sequential Decision Making）

在本文中我们将介绍序列决策（Sequential Decision Making）过程中的各个过程。

智能体与环境

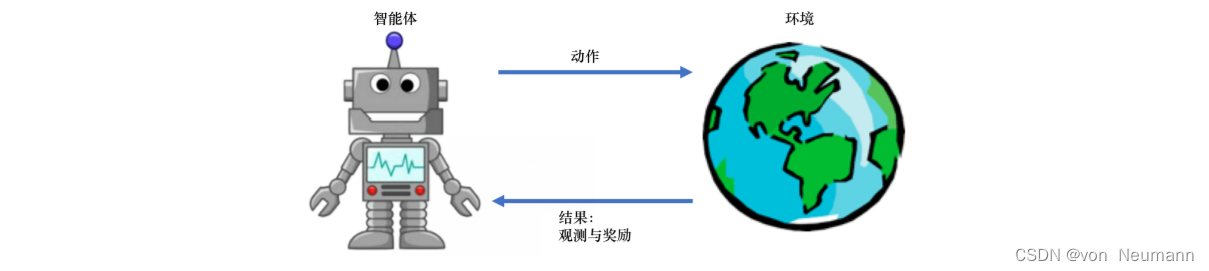
强化学习研究的问题是智能体与环境交互的问题，下图左边的智能体一直在与下图右边的环境进行交互。智能体把它的动作输出给环境，环境取得这个动作后会进行下一步，把下一步的观测与这个动作带来的奖励返还给智能体。这样的交互会产生很多观测，智能体的目的是从这些观测之中学到能最大化奖励的策略。
智能体与环境

奖励

奖励是由环境给的一种标量的反馈信号（Scalar Feedback Signal），这种信号可显示智能体在某一步采取某个策略的表现如何。强化学习的目的就是最大化智能体可以获得的奖励，智能体在环境里面存在的目的就是最大化它的期望的累积奖励（Expected Cumulative Reward）。不同的环境中，奖励也是不同的。这里给大家举一些奖励的例子：

比如一个象棋选手，他的目的是赢棋，在最后棋局结束的时候，他就会得到一个正奖励（赢）或者负奖励（输）
在股票管理里面，奖励由股票获取的奖励与损失决定
在玩雅达利游戏的时候，奖励就是增加或减少的游戏的分数，奖励本身的稀疏程度决定了游戏的难度。

序列决策

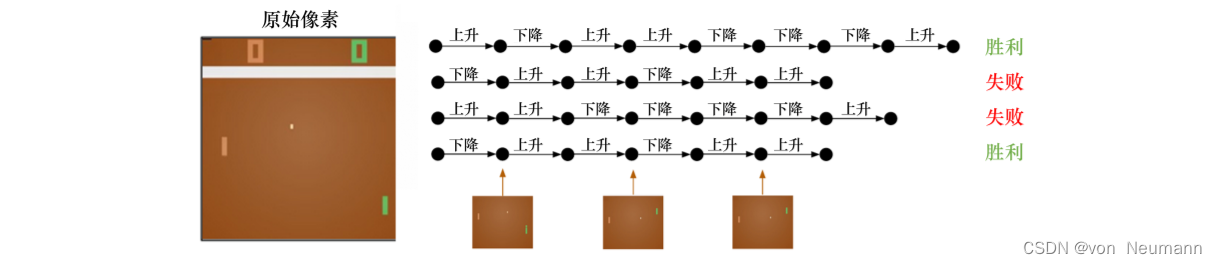
在一个强化学习环境里面，智能体的目的就是选取一系列的动作来最大化奖励，所以这些选取的动作必须有长期的影响。但在这个过程里面，智能体的奖励其实是被延迟了的，就是我们现在选取的某一步动作，可能要等到很久后才知道这一步到底产生了什么样的影响。如下图所示，在玩雅达利的Pong游戏时，我们可能只有到最后游戏结束时，才知道球到底有没有被击打过去。过程中我们采取的上升或下降动作，并不会直接产生奖励。强化学习里面一个重要的课题就是近期奖励和远期奖励的权衡，研究怎么让智能体取得更多的远期奖励。
Pong游戏

在与环境的交互过程中，智能体会获得很多观测。针对每一个观测，智能体会采取一个动作，也会得到一个奖励。所以历史是观测、动作、奖励的序列：
$H_t=o_1, a_1, r_1, o_2, a_2, r_2, \cdots, o_t, a_t, r_t$

智能体在采取当前动作的时候会依赖于它之前得到的历史，所以我们可以把整个游戏的状态看成关于这个历史的函数：
$S_t=f(H_t)$

状态是对世界的完整描述，不会隐藏世界的信息。观测是对状态的部分描述，可能会遗漏一些信息。在深度强化学习中，我们几乎总是用实值的向量、矩阵或者更高阶的张量来表示状态和观测。例如，我们可以用RGB像素值的矩阵来表示一个视觉的观测，可以用机器人关节的角度和速度来表示一个机器人的状态。

环境有自己的函数 $s^e_t=f(H_t^e)$ 来更新状态，在智能体的内部也有一个函数 $s^a_t=f(H_t^a)$ 来更新状态。当智能体的状态与环境的状态等价的时候，即当智能体能够观察到环境的所有状态时，我们称这个环境是完全可观测的（Fully Observed）。在这种情况下面，强化学习通常被建模成一个马尔可夫决策过程（Markov Decision Process，MDP）的问题。在马尔可夫决策过程中，我们有 $o_t=s^e_t=s^a_t$ 。

但是有一种情况是智能体得到的观测并不能包含环境运作的所有状态，因为在强化学习的设定里面，环境的状态才是真正的所有状态。比如智能体在玩Black Jack游戏，它能看到的其实是牌面上的牌。或者在玩雅达利游戏的时候，观测到的只是当前电视上面这一帧的信息，我们并没有得到游戏内部里面所有的运作状态。也就是当智能体只能看到部分的观测，我们就称这个环境是部分可观测的（Partially Observed）。在这种情况下，强化学习通常被建模成部分可观测马尔可夫决策过程（Partially Observable Markov Decision Process, POMDP）的问题。部分可观测马尔可夫决策过程是马尔可夫决策过程的一种泛化。部分可观测马尔可夫决策过程依然具有马尔可夫性质，但是假设智能体无法感知环境的状态，只能知道部分观测值。比如在自动驾驶中，智能体只能感知传感器采集的有限的环境信息。部分可观测马尔可夫决策过程可以用一个七元组描述： $\Omega, O, \gamma)$ ，其中 $S$ 表示状态空间，是一个隐变量， $A$ 为动作空间， $T (s^{'} ∣ s, a)$ 为状态转移概率， $R$ 为奖励函数， $\Omega(o|s, a)$ 为观测概率， $O$ 为观测空间， $\gamma$ 为折扣系数。