这篇文章主要想搞懂以下几个问题：

1、什么是自注意力（Self-Attention）

2、Q,K,V是什么

好了废话不多说，直接进入正题

Q,K,V分别代表query，key和value，这很容易让人联想到python的字典数据结构，假设我们有一个字典，存放着一个班级的身高（key）和体重（value）关系

{'160':50,'166':57,'173':65,'177':67,...}

这里取前三组，并以表格的形式展现：

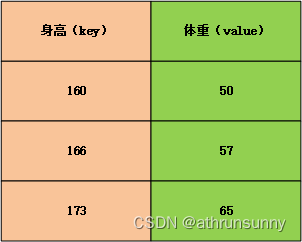
        假设接到一个查询（query）身高为162，该查询并未在字典中，想要通过已有的字典数据预测改身高下的体重信息，直观推断，该体重可能会在50-57之间。但是想要定量的计算体重的预测值，我们可以通过加权平均的方式进行求解。

162和160之间的距离为2，162与166之间的距离为4，160与166之间的距离为6，那么162->160取4/6的权重，162->166取2/6的权重。

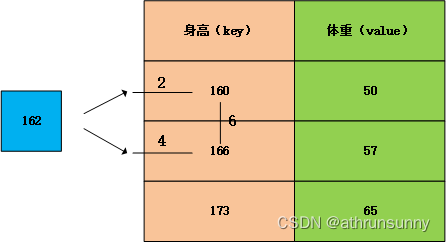
那么映射到体重上，对体重进行加权，就可以估计出162对应的体重约为50*（4/6）+57*（2/6）=52.33，接近50也符合预期。

因为162在[160,166]之间，所以这里很容易的为他们分配更多的权重，更加的注意他们，越近分配的权重越大，分别为他们分配了2/3和1/3的注意力权重。

但是在字典中，可能其他的键值对（key，value）对该query也存在影响，但是我们没有用上，那么要怎么用上字典中的所有数据，让估计的值更准确呢？

假设用一个函数来表示和所对应的注意力权重，那么体重的预测值可以用以下方式得出：

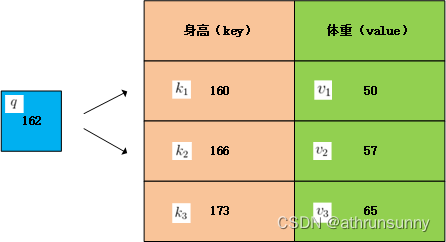
其中是能够表征相关性的函数，以高斯核为例，那么

其中为注意力分数，为注意力权重。

将对应的数值带入到公式中可得(其中的数字不是张量，所以用了x)

 

这样我们就可以利用上字典中其他的元素，通过身高来估计体重，这也就是注意力机制。

以上表示的是输入数据为一维的情况，当query，key，value为多维的情况也是类似的。

在介绍多维情况前先介绍注意力分数的计算方式有以下几种：

        目前大多的模型都是缩放点积模型，Transformer模型使用缩放点积注意力机制而不使用加性模型，这是因为缩放点积注意力在实际应用中表现更好。它具有更好的计算效率，适用于长序列，而且有更好的梯度传播性质，使得训练更加稳定。此设计是为了提高模型的性能和效率。这里以点积模型为例。

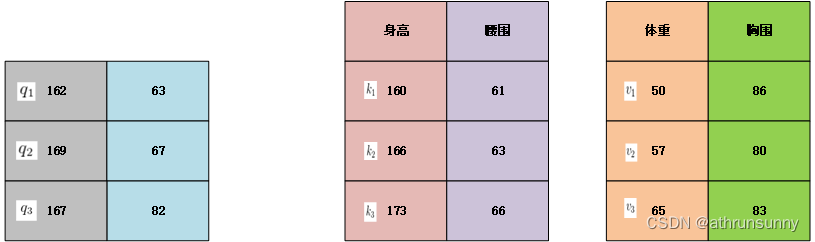
 对于和, 

其余的 和以及和以相同的方式处理。

那么就能得到： 

 

将其转换为矩阵形式：

 即：

还会除以一个特征维度将得分进行缩放，让梯度更稳定，乘法可能会产生梯度爆炸问题。

也就是：

这就是常见的缩放点积模型。经过softmax后，大值被放大，小值被抑制，这让模型能更加关注权重更大的地方。

如果其中的QKV都是同一个矩阵，那么他就是自注意模型了

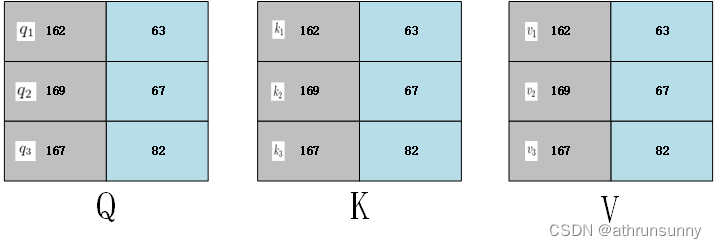
用表示其中的一个矩阵

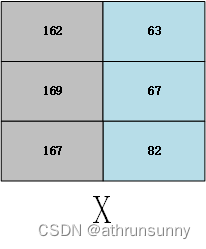
那么

直接这么做其实没有多大意义的，实际的transformer中会将QKV使用linear做线性变换（可学习参数），映射到不同的线性空间，并且会将其分成多个head，每个head能学到不同的东西，来增加特征的多样性，从而为模型提供更多的表达能力。

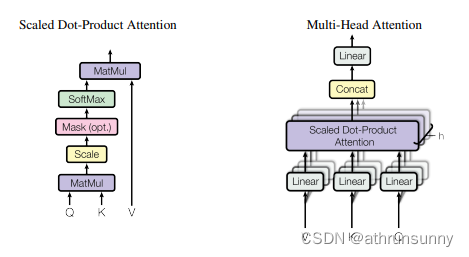
那么就能得到

也就是自注意模型的公式