摘要:本案例将主要结合自动售货机的实际情况,对销售的历史数据进行处理,利用pyecharts库、Matplotlib库进行可视化分析,并对未来4周商品的销售额进行预测,从而为企业制定相应的自动售货机市场需求分析及销售建议提供参考依据。更多详细内容请参考《Python数据挖掘:入门进阶与实用案例分析》一书。

01案例背景
近年来,随着我国经济技术的不断提升,自动化机械在人们日常生活中扮演着越来越重要的角色,更多的被应用在不同的领域。而作为新的一种自动化零售业态,自动售货机在日常生活中应用越来越广泛。自动售货机销售产业在走向信息化、合理化同时,也面临着高度同质化、成本上升、毛利下降等诸多困难与问题,这也是大多数企业所会面临到的问题。
为了提高市场占有率和企业的竞争力,某企业在广东省某8个市部署了376台自动售货机,但经过一段时间后,发现其经营状况并不理想。而如何了解销售额、订单数量与自动售货机数量之间的关系,畅销或滞销的商品又有哪些,自动售货机的销售情况等,已成为该企业亟待解决的问题。
02分析目标
获取了该企业某6个月的自动售货机销售数据,结合销售背景进行分析,并可视化展现销售现状,同时预测未来一段时间内的销售额,从而为企业制定营销策略提供一定的参考依据。
03 分析过程
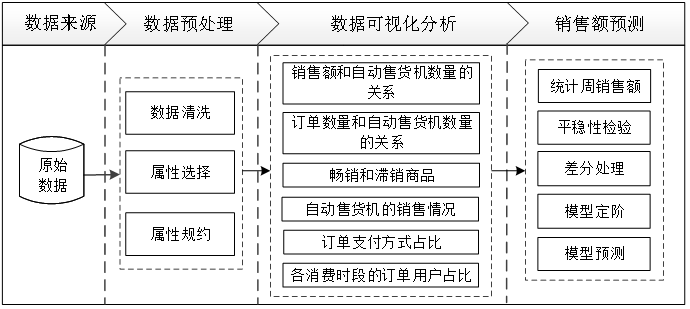
04 数据预处理
1. 清洗数据
1.1 合并订单表并处理缺失值
由于订单表的数据是按月份分开存放的,为了方便后续对数据进行处理和可视化,所以需要对订单数据进行合并处理。同时,在合并订单表的数据后,为了了解订单表的缺失数据的基本情况,需要进行缺失值检测。合并订单表并进行缺失值检测,操作结果如图1所示。
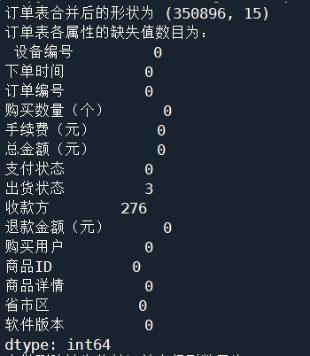
图1 合并订单表并进行缺失值检测的结果
由操作结果可知,合并后的订单数据有350867条记录,且订单表中含有缺失值的记录总共有279条,其数量相对较少,可直接使用删除法对其中的缺失值进行处理。
合并订单表、查看缺失值并处理缺失值,如代码清单1所示。
代码清单1 合并订单表、查看缺失值并处理缺失值
import pandas as pd# 读取数据
data4 = pd.read_csv('../data/订单表2018-4.csv', encoding='gbk')
data5 = pd.read_csv('../data/订单表2018-5.csv', encoding='gbk')
data6 = pd.read_csv('../data/订单表2018-6.csv', encoding='gbk')
data7 = pd.read_csv('../data/订单表2018-7.csv', encoding='gbk')
data8 = pd.read_csv('../data/订单表2018-8.csv', encoding='gbk')
data9 = pd.read_csv('../data/订单表2018-9.csv', encoding='gbk')# 合并数据data = pd.concat([data4, data5, data6, data7, data8, data9], ignore_index=True)
print('订单表合并后的形状为', data.shape)
# 缺失值检测
print('订单表各属性的缺失值数目为:\n', data.isnull().sum())
data = data.dropna(how='any') # 删除缺失值1.2 增加“市”属性
为了满足后续的数据可视化需求,需要在订单表中增加“市”属性,操作结果如图2所示。
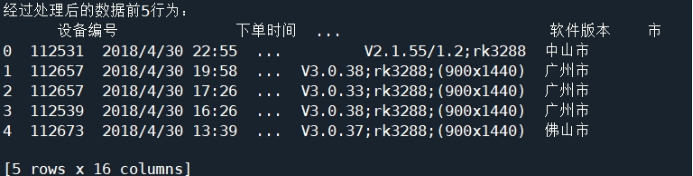
图2 增加“市”属性
增加“市”属性如代码清单2所示。
代码清单2 增加“市”属性
| # 从省市区属性中提取市的信息,并创建新属性 data['市'] = data['省市区'].str[3: 6] print('经过处理后的数据前5行为:\n', data.head()) |
1.3 处理订单表中的“商品详情”属性
通过浏览订单表数据发现,在“商品详情”属性中存在有异名同义的情况,即两个名称不同的值所代表的实际意义是一致的,如“脉动青柠X1;”“脉动青柠x1;”等。因为此情况会对后面的分析结果造成一定的影响,所以需要对订单表中的“商品详情”属性进行处理,增加“商品名称”属性,如代码清单3所示。
代码清单3 处理订单表中的“商品详情”属性
| # 定义一个需剔除字符的列表error_str error_str = [' ', '(', ')', '(', ')', '0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'g', 'l', 'm', 'M', 'L', '听', '特', '饮', '罐', '瓶', '只', '装', '欧', '式', '&', '%', 'X', 'x', ';'] # 使用循环剔除指定字符 for i in error_str: data['商品详情'] = data['商品详情'].str.replace(i, '') # 新建“商品名称”属性,用于新数据的存放 data['商品名称'] = data['商品详情'] |
1.4 处理“总金额(元)”属性
此外,当浏览订单表数据时,发现在“总金额(元)”属性中,存在极少订单的金额很小,如0、0.01等。在现实生活中,这种记录存在的情况极少,且这部分数据不具有分析意义。因此,在本案例中,对订单的金额小于0.5的记录进行删除处理,操作结果如图3所示。
![]()
图3删除后的数据量
由操作结果可知,删除前的数据行列数目为(350617, 17),删除后的数据行列数目为(350450, 17)。
删除“总金额(元)”属性中订单的金额较少的记录如代码清单4所示。
代码清单4 删除“总金额(元)”属性中订单的金额较少的记录
| # 删除金额较少的订单前的数据行列数目 print(data.shape) # 删除金额较少的订单后的数据行列数目 data = data[data['总金额(元)'] >= 0.5] print(data.shape) |
2.属性选择
因为订单表中的“手续费(元)”“收款方”“软件版本”“省市区”“商品详情”“退款金额(元)”等属性对本案例的分析没有意义,所以需要对其进行删除处理,选择合适的属性,操作的结果如图4所示。

图4属性选择
属性选择如代码清单5所示。
代码清单5 属性选择
| # 对于订单表数据选择合适的属性 data = data.drop(['手续费(元)', '收款方', '软件版本', '省市区', '商品详情', '退款金额(元)'], axis=1) print('选择后,数据属性为:\n', data.columns.values) |
3.属性规约
在订单表“下单时间”属性中含有的信息量较多,并且存在概念分层的情况,需要对属性进行数据规约,提取需要的信息。提取相应的“小时”属性和“月份”属性,进一步泛化“小时”属性为“下单时间段”属性,规则如下:
Ø当小时≤5时,为“凌晨”;
Ø当5<小时≤8时,为“早晨”;
Ø当8<小时≤11时,为“上午”;
Ø当11<小时≤13时,为“中午”;
Ø当13<小时≤16时,为“下午”;
Ø当16<小时≤19时,为“傍晚”;
Ø当19<小时≤24,为“晚上”。
在Python中规约订单表的属性,如代码清单6所示。
代码清单6 规约订单表的属性
| # 将时间格式的字符串转换为标准的时间格式 data['下单时间'] = pd.to_datetime(data['下单时间']) data['小时'] = data['下单时间'].dt.hour # 提取时间中的小时 data['月份'] = data['下单时间'].dt.month # 提取时间中的月份 data['下单时间段'] = 'time' # 新增“下单时间段”属性,并将其初始化为time exp1 = data['小时'] <= 5 # 判断小时是否小于等于5 # 若条件为真,则时间段为凌晨 data.loc[exp1, '下单时间段'] = '凌晨' # 判断小时是否大于5且小于等于8 exp2 = (5 < data['小时']) & (data['小时'] <= 8) # 若条件为真,则时间段为早晨 data.loc[exp2, '下单时间段'] = '早晨' # 判断小时是否大于8且小于等于11 exp3 = (8 < data['小时']) & (data['小时'] <= 11) # 若条件为真,则时间段为上午 data.loc[exp3, '下单时间段'] = '上午' # 判断小时是否小大于11且小于等于13 exp4 = (11 < data['小时']) & (data['小时'] <= 13) # 若条件为真,则时间段为中午 data.loc[exp4, '下单时间段'] = '中午' # 判断小时是否大于13且小于等于16 exp5 = (13 < data['小时']) & (data['小时'] <= 16) # 若条件为真,则时间段为下午 data.loc[exp5, '下单时间段'] = '下午' # 判断小时是否大于16且小于等于19 exp6 = (16 < data['小时']) & (data['小时'] <= 19) # 若条件为真,则时间段为傍晚 data.loc[exp6, '下单时间段'] = '傍晚' # 判断小时是否大于19且小于等于24 exp7 = (19 < data['小时']) & (data['小时'] <= 24) # 若条件为真,则时间段为晚上 data.loc[exp7, '下单时间段'] = '晚上' data.to_csv('../tmp/order.csv', index=False, encoding = 'gbk') |
05 销售数据可视化分析
在销售数据中含有的数据量较多,作为企业管理人员以及决策制定者,无法直观了解目前自动售货机的销售状况。因此需要利用处理好的数据进行可视化分析,直观地展示销售走势以及各区销售情况等,为决策者提供参考。
1.销售额和自动售货机数量的关系
探索6个月销售额和自动售货机数量之间的关系,并按时间走势进行可视化分析,结果如图5所示。
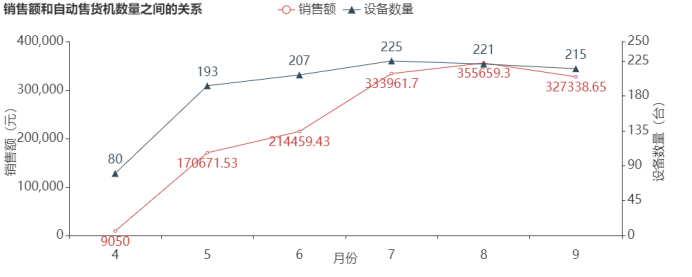
图5 销售额和自动售货机数量之间的关系
由图5可知,4月至7月,自动售货机的数量在增加,销售额也随着自动售货机的数量增加而增加;8月,虽然自动售货机数量减少了4台,但是销售额还在增加;9月相比8月的自动售货机数量减少了6台,销售额也随着减少。可以推断出销售额与自动售货机的数量存在一定的相关性,增加自动售货机的数量将会带来销售额的增长。出现该情况可能是因为广东处于亚热带,气候相对炎热,而7、8、9月的气温也相对较高,人们使用自动售货机的频率也相对较高。
探索销售额和自动售货机数量之间的关系如代码清单7所示。
代码清单7 销售额和自动售货机数量之间的关系
| import pandas as pd import numpy as np from pyecharts.charts import Line from pyecharts import options as opts import matplotlib.pyplot as plt from pyecharts.charts import Bar from pyecharts.charts import Pie from pyecharts.charts import Grid data = pd.read_csv('../tmp/order.csv', encoding='gbk') def f(x): return len(list(set((x.values)))) # 绘制销售额和自动售货机数量之间的关系图 groupby1 = data.groupby(by='月份', as_index=False).agg({'设备编号': f, '总金额(元)': np.sum}) groupby1.columns = ['月份', '设备数量', '销售额'] line = (Line() .add_xaxis([str(i) for i in groupby1['月份'].values.tolist()]) .add_yaxis('销售额', np.round(groupby1['销售额'].values.tolist(), 2)) .add_yaxis('设备数量', groupby1['设备数量'].values.tolist(), yaxis_index=1,symbol='triangle') .set_series_opts(label_opts=opts.LabelOpts(is_show=True, position='top', font_size=10)) .set_global_opts( xaxis_opts=opts.AxisOpts(name='月份', name_location='center', name_gap=25), title_opts=opts.TitleOpts(title='销售额和自动售货机数量之间的关系'), yaxis_opts=opts.AxisOpts( name='销售额(元)', name_location='center', name_gap=60, axislabel_opts=opts.LabelOpts( formatter='{value}'))) .extend_axis( yaxis=opts.AxisOpts( name='设备数量(台)', name_location='center', name_gap=40, axislabel_opts=opts.LabelOpts( formatter='{value}'), interval=50)) ) line.render_notebook() |
2.订单数量和自动售货机数量的关系
探索6个月订单数量和自动售货机数量之间的关系,并按时间走势进行可视化分析,结果如图6所示。
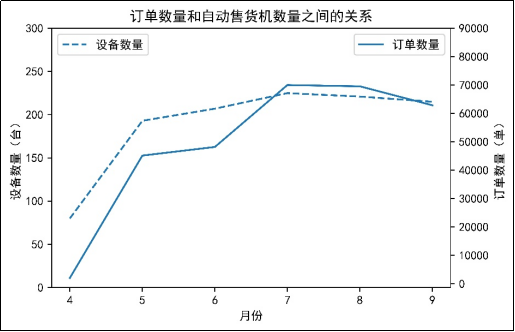
图6 订单数量和自动售货机数量之间的关系
由图6可知,4月至7月,自动售货机数量呈上升趋势,订单数量也随着自动售货机数量增加而增加,而8月至9月,自动售货机数量在减少,订单数量也在减少。这说明了订单数量与自动售货机的数量是严格相关的,增加自动售货机会给用户带来便利,从而提高订单数量。同时,结合图5可知,订单数量和销售额的变化趋势基本保持一样的变化趋势,这也说明了订单数量和销售额存在一定的相关性。
由于各市的设备数量并不一致,所以探索各市自动售货机的平均销售总额,并进行对比分析,结果如图7所示。
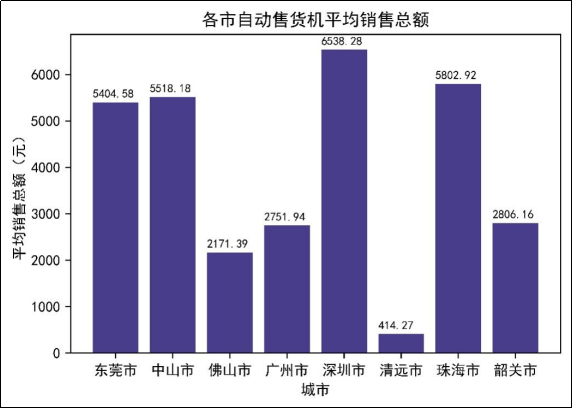
图7 各市自动售货机平均销售总额
由图7可知,深圳市自动售货机平均销售总额最高,达到了6538.28元,排在其后的是珠海市和中山市。而最少的是清远市,其平均销售总额只有414.27元。出现此情况可能是因为不同区域的人流量不同,而深圳市相对于其他区域的人流量相对较大,清远市相对于其他区域的人流量相对较小。此外,广州市的人流量也相对较大,但其平均销售总额却相对较少,可能是因为自动售货机放置不合理导致的。
探索订单数量和自动售货机数量之间的关系,以及各市自动售货机的平均销售总额如代码清单8所示。
代码清单8 订单数量和自动售货机数量之间的关系
| groupby2 = data.groupby(by='月份', as_index=False).agg({'设备编号': f, '订单编号': f}) groupby2.columns = ['月份', '设备数量', '订单数量'] # 绘制图形 plt.figure(figsize=(10, 4)) plt.rcParams['font.sans-serif'] = ['SimHei'] plt.rcParams['axes.unicode_minus'] = False fig, ax1 = plt.subplots() # 使用subplots函数创建窗口 ax1.plot(groupby2['月份'], groupby2['设备数量'], '--') ax1.set_yticks(range(0, 350, 50)) # 设置y1轴的刻度范围 ax1.legend(('设备数量',), loc='upper left', fontsize=10) ax2 = ax1.twinx() # 创建第二个坐标轴 ax2.plot(groupby2['月份'], groupby2['订单数量']) ax2.set_yticks(range(0, 100000, 10000)) # 设置y2轴的刻度范围 ax2.legend(('订单数量',), loc='upper right', fontsize=10) ax1.set_xlabel('月份') ax1.set_ylabel('设备数量(台)') ax2.set_ylabel('订单数量(单)') plt.title('订单数量和自动售货机数量之间的关系') plt.show() gruop3 = data.groupby(by='市', as_index=False).agg({'总金额(元)':sum, '设备编号':f}) gruop3['销售总额'] = np.round(gruop3['总金额(元)'], 2) gruop3['平均销售总额'] = np.round(gruop3['销售总额'] / gruop3['设备编号'], 2) plt.bar(gruop3['市'].values.tolist(), gruop3['平均销售总额'].values.tolist(), color='#483D8B') # 添加数据标注 for x, y in enumerate(gruop3['平均销售总额'].values): plt.text(x - 0.4, y + 100, '%s' %y, fontsize=8) plt.xlabel('城市') plt.ylabel('平均销售总额(元)') plt.title('各市自动售货机平均销售总额') plt.show() |
3.畅销和滞销商品
查找6个月销售额排名前10和后10的商品,从而找出畅销商品和滞销商品,并对其销售额进行可视化分析,结果如图8、图9所示。
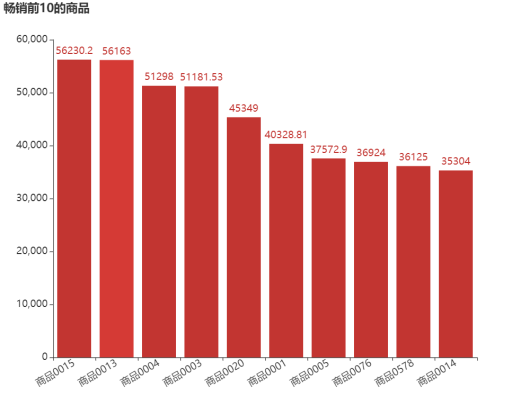
图8 销售额前10的商品
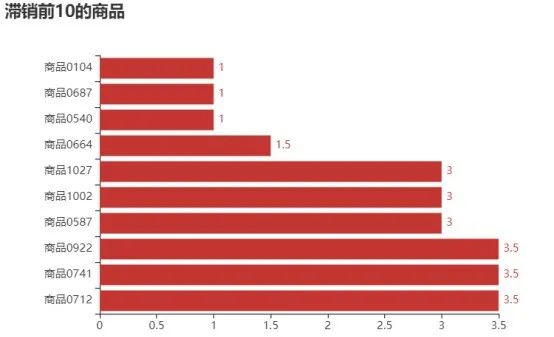
图9 销售额后10的商品
由图8可知,销售额排在第一的是商品0015,达到了56230.2元,其次是商品0013和商品0004等商品。由图9可知,销售额排在最后的商品是商品0104、商品0687和商品0540,其销售金额只有1元。
探索6个月销售额排名前10和后10的商品如代码清单9所示。
代码清单9 10种畅销商品、10种滞销商品
| # 销售额前10的商品 group4 = data.groupby(by='商品ID', as_index=False)['总金额(元)'].sum() group4.sort_values(by='总金额(元)', ascending=False, inplace=True) d = group4.iloc[: 10] x_data = d['商品ID'].values.tolist() y_data = np.round(d['总金额(元)'].values, 2).tolist() bar = (Bar(init_opts=opts.InitOpts(width='800px',height='600px')) .add_xaxis(x_data) .add_yaxis('', y_data, label_opts=opts.LabelOpts(font_size=15)) .set_global_opts(title_opts=opts.TitleOpts(title='畅销前10的商品'), yaxis_opts=opts.AxisOpts(axislabel_opts=opts.LabelOpts( formatter='{value}',font_size=15)), xaxis_opts=opts.AxisOpts(type_='category', axislabel_opts=opts.LabelOpts({'interval': '0'}, font_size=15, rotate=30)))) bar.render_notebook() h = group4.iloc[-10: ] x_data = h['商品ID'].values.tolist() y_data = np.round(h['总金额(元)'].values, 2).tolist() bar = (Bar() .add_xaxis(x_data) .add_yaxis('', y_data, label_opts=opts.LabelOpts(position='right')) .set_global_opts(title_opts=opts.TitleOpts( title='滞销前10的商品'), xaxis_opts=opts.AxisOpts( axislabel_opts={'interval': '0'})) .reversal_axis() ) grid = Grid(init_opts=opts.InitOpts(width='600px', height='400px')) grid.add(bar, grid_opts=opts.GridOpts(pos_left='18%')) grid.render_notebook() |
4.自动售货机的销售情况
探索6个月销售额前10以及销售额后10的设备及其所在的城市,并进行可视化分析,结果如图10、图11所示。
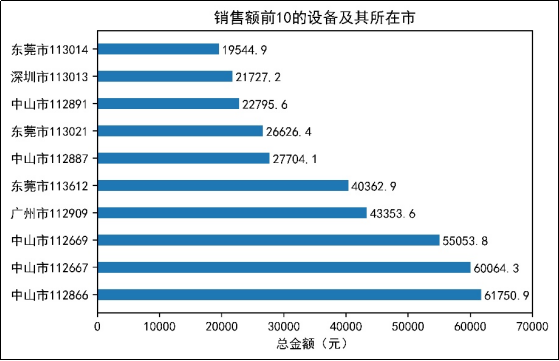
图10 销售额前10的设备及其所在市
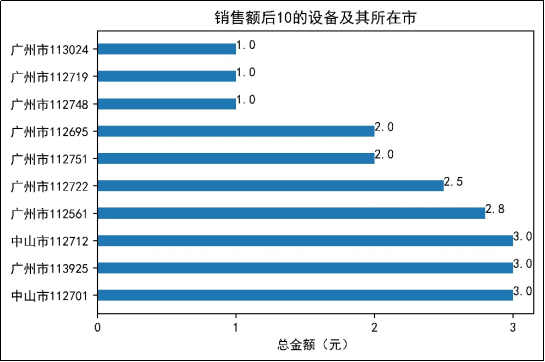
图11 销售额后10的设备及其所在市
由图10可知,销售额靠前的设备所在城市主要集中在中山市、广州市、东莞市和深圳市,其中,销售额前3的设备都集中在中山市。由图11可知,广州市的设备113024、112719、112748的销售额只有1元,而销售额后10的设备全部在广州市和中山市。
探索6个月销售额前10以及销售额后10的设备及其所在的城市如代码清单10所示。
代码清单10 销售额前10、后10的设备及其所在市
| group5 = data.groupby(by=['市', '设备编号'], as_index=False)['总金额(元)'].sum() group5.sort_values(by='总金额(元)', ascending=False, inplace=True) b = group5[: 10] label = [] # 销售额前10的设备及其所在市 for i in range(len(b)): a = b.iloc[i, 0] + str(b.iloc[i, 1]) label.append(a) x = np.round(b['总金额(元)'], 2).values.tolist() y = range(10) plt.bar(x=0, bottom=y, height=0.4, width=x, orientation='horizontal') plt.xticks(range(0, 80000, 10000)) # 设置x轴的刻度范围 plt.yticks(range(10), label) for y, x in enumerate(np.round(b['总金额(元)'], 2).values): plt.text(x + 500, y - 0.2, "%s" %x) plt.xlabel('总金额(元)') plt.title('销售额前10的设备及其所在市') plt.show() l = group5[-10: ] label1 = [] for i in range(len(l)): a = l.iloc[i, 0] + str(l.iloc[i, 1]) label1.append(a) x = np.round(l['总金额(元)'], 2).values.tolist() y = range(10) plt.bar(x=0, bottom=y, height=0.4, width=x, orientation='horizontal') plt.xticks(range(0, 4, 1)) # 设置x轴的刻度范围 plt.yticks(range(10), label1) for y, x in enumerate(np.round(l['总金额(元)'], 2).values): plt.text(x, y, "%s" %x) plt.xlabel('总金额(元)') plt.title('销售额后10的设备及其所在市') plt.show() |
统计各城市销售额小于100的设备数量,并进行可视化分析,结果如图12所示。
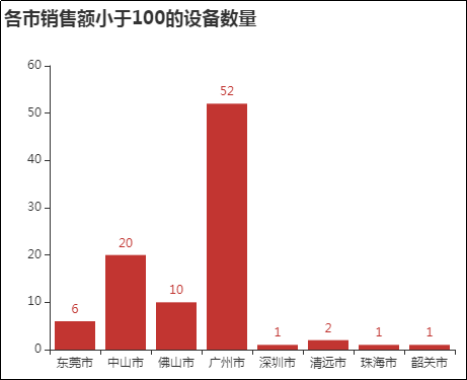
图12 各市销售额小于100的设备数量
由图12可知,销售额小于100的设备在广州市有52台,中山市有20台,佛山市有10台。出现这种情况的原因可能是设备放置位置的不合理,或设备放置过多造成的,因此可以适当调整自动售货机放置的位置和数量,减少设备和人员的浪费。
探索各城市销售额小于100元的设备数量如代码清单11所示。
代码清单11 各城市销售额小于100元的设备数量
| l_b = group5[group5['总金额(元)'] < 100] lb = l_b.groupby(by='市', as_index=False)['设备编号'].count() x_data = lb['市'].values.tolist() y_data = lb['设备编号'].values.tolist() bar = (Bar(init_opts=opts.InitOpts(width='500px', height='400px')) .add_xaxis(x_data) .add_yaxis('', y_data) .set_global_opts(title_opts=opts.TitleOpts( title='各市销售额小于100的设备数量')) ) bar.render_notebook() |
5.订单支付方式占比
对自动售货机上各商品订单的支付方式进行统计,并进行可视化分析,结果如图13所示。
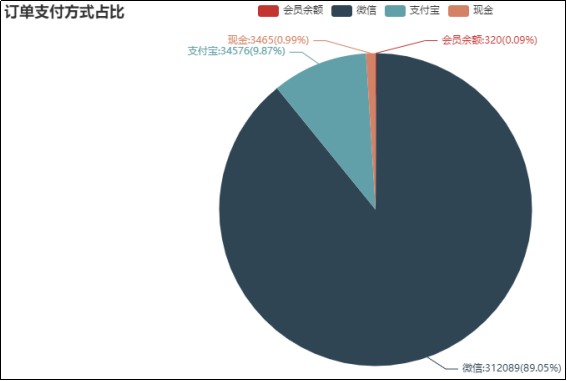
图13 订单支付方式占比
由图13可知,订单的主要支付方式有4种,即微信、支付宝、会员余额和现金,其中支付方式最多的是微信支付,在所有支付方式中占到了89.05%。其次是支付宝支付,其占比为9.87%,而现金支付和会员余额支付的占比不到1%。
分析订单支付方式占比如代码清单12所示。
代码清单12 分析订单支付方式占比
| group6 = data.groupby(by='支付状态')['支付状态'].count() method = group6.index.tolist() num = group6.values.tolist() pie_data = [(i, j) for i, j in zip(method, num)] pie = (Pie() .add('', pie_data, label_opts=opts.LabelOpts(formatter='{b}:{c}({d}%)')) .set_global_opts(title_opts=opts.TitleOpts(title='订单支付方式占比'))) pie.render_notebook() |
6.各消费时段的订单用户占比
在自动售货机的商品下单时间段上,统计各消费时段的订单用户数量,并进行可视化分析,结果如图14所示。
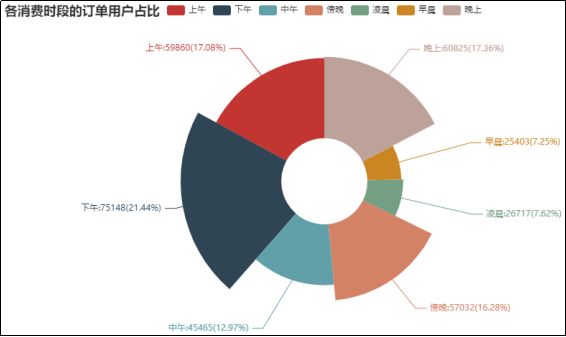
图14 各消费时段的订单用户占比
由图14可知,当消费时间段在下午时,其订单用户最多,占比达到了21.44%,其次是晚上,占比是17.36%,上午的占比也有17.08%,其余时间段的占比相对较少。
分析各消费时段的订单用户如代码清单13所示。
代码清单13 分析各消费时段的订单用户
| group7 = data.groupby(by='下单时间段')['购买用户'].count() times = group7.index.tolist() num = group7.values.tolist() pie_data_2 = [(i, j) for i, j in zip(times, num)] pie = (Pie() .add('', pie_data_2, label_opts=opts.LabelOpts(formatter='{b}:{c}({d}%)'), radius=[60, 200], rosetype='radius', is_clockwise=False) .set_global_opts(title_opts=opts.TitleOpts(title='各消费时段的订单用户占比')) ) pie.render_notebook() |
06 销售额预测
精准的销售额预测对于企业运营有着非常重要的指导意义,可以指导运营后台提前进行合理的资源配置,帮助企业管理人员制定合理的目标。同时,还可以更好地帮助企业采取更为针对性的促销手段,更加明确市场的需求,可以根据不同区域、不同时间划分等制定更加有效、合理的配货方案和商品价格,从而增加企业经营收益。
自动售货机的销售额预测指的是从售货机已有销售额的订单数据资料中,总结出商品销售额的变化规律,并根据该规律构建ARIMA模型,动态预测未来4周内商品的销售额。
ARIMA模型的建模步骤如图15所示。
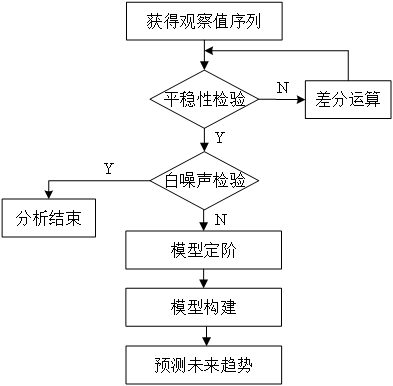
图15 ARIMA模型的建模步骤
1.统计周销售额
通过观察订单数据,发现该数据集记录的是当前日期时间下,售货机所售卖商品的订单状况,其出货状态有出货成功、出货失败、未出货等多种情况。然而,为预测未来4周的销售额,其所需样本数据应为实际的周销售额数据,因此,需要筛选状态为出货成功的数据并统计各周销售额,如代码清单14所示。
代码清单14 筛选出货成功数据并统计各周销售额
| import pandas as pd import matplotlib.pyplot as plt from statsmodels.tsa.stattools import adfuller as ADF from statsmodels.graphics.tsaplots import plot_acf from statsmodels.stats.diagnostic import acorr_ljungbox from statsmodels.tsa.arima_model import ARIMA data = pd.read_csv('../tmp/order.csv', encoding='gbk') # 提取出货状态为“出货成功”的下单时间和总金额(元)数据 data_info = data.loc[data['出货状态'] == '出货成功', ['下单时间', '总金额(元)']] data_info = data_info.set_index('下单时间') # 将下单时间设为索引 # 将索引修改为日期时间格式 data_info.index = pd.to_datetime(data_info.index) # 按周对总金额进行汇总,即求和 data_w = data_info.resample('W').sum() |
2.平稳性检验
在使用ARIMA模型进行销售额预测之前,需要查看时间序列是否平稳,若数据非平稳,在数据分析挖掘的时候,则可能会产生“伪回归”等问题,从而影响分析结果。通过时间序列的时序图、自相关图及其单位根查看时间序列平稳性,时序图如图16所示,自相关图如图17所示,单位根检验结果如图18所示。
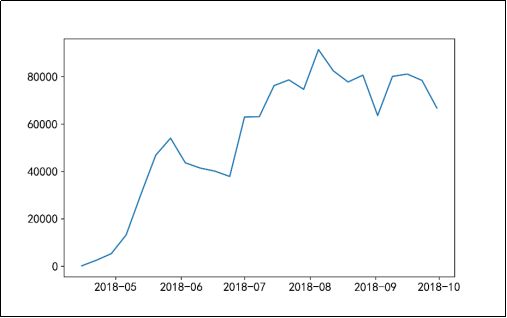
图16 原始序列的时序图
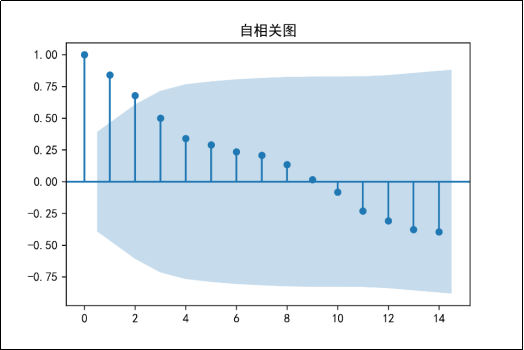
图17 原始序列的自相关图
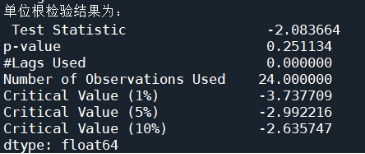
图18 原始序列的单位根检验结果
由图16可知,时序图显示该序列具有明显的递增趋势,可以判断为原始序列数据是非平稳序列;图17的自相关图显示的自相关系数大部分均大于零,说明序列间具有一定的长期相关性。由图18可知,在单位根检验统计量中,p值为0.251134,其值显著大于0.05,可以推断出该序列为非平稳序列(非平稳序列一定不是白噪声序列)。
绘制时序图、自相关图并进行单位根检验如代码清单15所示。
代码清单15 绘制时序图、自相关图并进行单位根检验
| # 平稳性检验 # 判断是否为时间序列 plt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文标签 plt.rcParams['axes.unicode_minus'] = False # 显示负号 plt.figure(figsize=(8, 5)) plt.plot(data_w) plt.tick_params(labelsize=14) # 设置坐标轴字体大小 plt.show() # 定义绘制自相关图函数 def draw_acf(ts): plt.figure(facecolor='white', figsize=(10, 8)) plot_acf(ts) plt.show() # 定义单位根检验函数 def testStationarity(ts): dftest = ADF(ts) # 对ADF求得的值进行语义描述 dfoutput = pd.Series(dftest[0:4], index = ['Test Statistic','p-value','#Lags Used', 'Number of Observations Used']) for key, value in dftest[4].items(): dfoutput['Critical Value (%s)'%key] = value return dfoutput # 自相关 draw_acf(data_w) # 单位根检验 print('单位根检验结果为:\n', testStationarity(data_w)) |
3.差分处理
在进行平稳性检验后,发现原始序列数据属于非平稳序列,而在使用ARIMA模型进行销售额预测时,需要序列数据是平稳序列,以避免序列中的随机游走形势影响预测结果。在Python中,可以通过二阶差分处理对数据进行平稳化操作,并查看二阶差分之后序列的平稳性和白噪声,其中二阶差分后序列的时序图如图19所示,二阶差分后序列的自相关图如图20所示,二阶差分后序列的单位根检验结果如图21所示,二阶差分后序列的白噪声检验结果如图22所示。
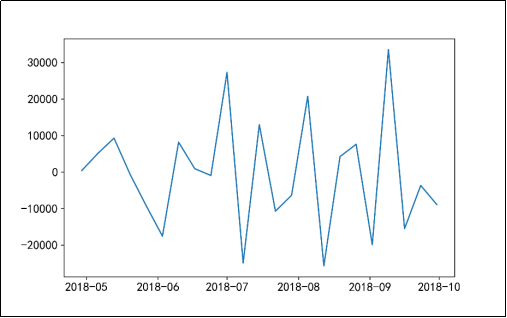
图19 二阶差分后序列的时序图
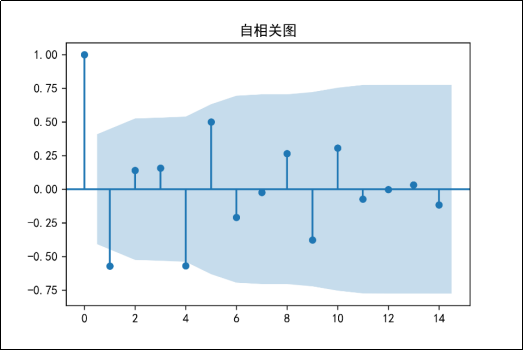
图20 二阶差分后序列的自相关图
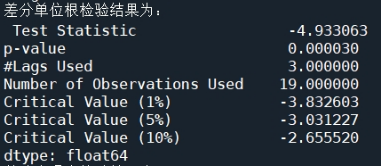
图21 二阶差分后序列的单位根检验结果
![]()
图22 二阶差分后序列的白噪声检验结果
由图19可知,该序列无明显趋势,较为稳定;图20的自相关图显示自相关系数较为均匀,且较为接近于0,有较强的短期相关性。由图21可知,二阶差分后序列的单位根检验p值远小于0.05,可以判断出差分处理后的序列是平稳序列。由图22可知,在白噪声检验结果中,输出的p值小于0.05,同时结合单位根检验结果可以判断二阶差分之后的序列是平稳非白噪声序列。
差分处理并查看序列平稳性和白噪声如代码清单16所示。
代码清单16 差分处理并查看序列平稳性和白噪声
| # 二阶差分处理 data_w_T1 = data_w.diff().dropna() data_w_T2 = data_w_T1.diff().dropna() # 差分后的时间序列图 plt.figure(figsize=(8, 5)) plt.plot(data_w_T2) plt.tick_params(labelsize=14) plt.show() # 差分自相关 draw_acf(data_w_T2) # 差分单位根检验 print('差分单位根检验结果为:\n', testStationarity(data_w_T2)) # 白噪声检验 print('差分白噪声检验结果为:\n', acorr_ljungbox(data_w_T2, lags=1)) |
4.模型定阶
通常情况下,在进行模型预测前,需要寻找最优模型,以提高预测结果的准确性。针对ARIMA模型,可以通过BIC矩阵进行模型定阶。由于4.4.3小节进行了二阶差分处理,所以d=2。通过计算ARIMA(p,2,q)中所有组合的BIC信息量,取最小BIC信息量所对应的模型阶数,进而确定p值和q值,结果如图23所示。
![]()
图23 模型定阶
由操作结果可知,当p值为0、q值为1时,BIC值最小,到此p、q定阶完成。
模型定阶如代码清单17所示。
代码清单17 模型定阶
| # 通过BIC矩阵进行模型定阶 data_w = data_w.astype(float) pmax = 3 qmax = 3 bic_matrix = [] # 初始化BIC矩阵 for p in range(pmax+1): tmp = [] for q in range(qmax+1): try: tmp.append(ARIMA(data_w, (p, 2, q)).fit().bic) except: tmp.append(None) bic_matrix.append(tmp) bic_matrix = pd.DataFrame(bic_matrix) # 找出最小值位置 p, q = bic_matrix.stack().idxmin() print('当BIC最小时,p值和q值分别为: ', p, q) |
5.模型预测
应用ARIMA(0, 2, 1)模型对未来4周内商品的销售额进行预测,结果如图24所示。

图24预测未来4周的销售额
预测未来4周内商品的销售额如代码清单18所示。
代码清单18 预测未来4周内商品的销售额
| # 构建ARIMA(0, 2, 1)模型 model = ARIMA(data_w, (p, 2, q)).fit() # 预测未来4周的销售额 print('预测未来4周的销售额,其预测结果、标准误差、置信区间如下。\n', model.forecast(4)) |
注:利用ARIMA模型向前预测的周期越长,其误差越大。
推荐阅读

正版链接:https://item.jd.com/13814157.html
《Python数据挖掘:入门、进阶与实用案例分析》是一本以项目实战案例为驱动的数据挖掘著作,它能帮助完全没有Python编程基础和数据挖掘基础的读者快速掌握Python数据挖掘的技术、流程与方法。在写作方式上,与传统的“理论与实践结合”的入门书不同,它以数据挖掘领域的知名赛事“泰迪杯”数据挖掘挑战赛(已举办10届)和“泰迪杯”数据分析技能赛(已举办5届)(累计1500余所高校的10余万师生参赛)为依托,精选了11个经典赛题,将Python编程知识、数据挖掘知识和行业知识三者融合,让读者在实践中快速掌握电商、教育、交通、传媒、电力、旅游、制造等7大行业的数据挖掘方法。
本书不仅适用于零基础的读者自学,还适用于教师教学,为了帮助读者更加高效地掌握本书的内容,本书提供了以下10项附加价值:
(1)建模平台:提供一站式大数据挖掘建模平台,免配置,包含大量案例工程,边练边学,告别纸上谈兵
(2)视频讲解:提供不少于600分钟Python编程和数据挖掘相关教学视频,边看边学,快速收获经验值
(3)精选习题:精心挑选不少于60道数据挖掘练习题,并提供详细解答,边学边练,检查知识盲区
(4)作者答疑:学习过程中有任何问题,通过“树洞”小程序,纸书拍照,一键发给作者,边问边学,事半功倍
(5)数据文件:提供各个案例配套的数据文件,与工程实践结合,开箱即用,增强实操性
(6)程序代码:提供书中代码的电子文件及相关工具的安装包,代码导入平台即可运行,学习效果立竿见影
(7)教学课件:提供配套的PPT课件,使用本书作为教材的老师可以申请,节省备课时间
(8)模型服务:提供不少于10个数据挖掘模型,模型提供完整的案例实现过程,助力提升数据挖掘实践能力
(9)教学平台:泰迪科技为本书提供的附加资源提供一站式数据化教学平台,附有详细操作指南,边看边学边练,节省时间
(10)就业推荐:提供大量就业推荐机会,与1500+企业合作,包含华为、京东、美的等知名企业
通过学习本书,读者可以理解数据挖掘的原理,迅速掌握大数据技术的相关操作,为后续数据分析、数据挖掘、深度学习的实践及竞赛打下良好的技术基础。
06 销售额预测
精准的销售额预测对于企业运营有着非常重要的指导意义,可以指导运营后台提前进行合理的资源配置,帮助企业管理人员制定合理的目标。同时,还可以更好地帮助企业采取更为针对性的促销手段,更加明确市场的需求,可以根据不同区域、不同时间划分等制定更加有效、合理的配货方案和商品价格,从而增加企业经营收益。
自动售货机的销售额预测指的是从售货机已有销售额的订单数据资料中,总结出商品销售额的变化规律,并根据该规律构建ARIMA模型,动态预测未来4周内商品的销售额。
ARIMA模型的建模步骤如图15所示。

图15 ARIMA模型的建模步骤
1.统计周销售额
通过观察订单数据,发现该数据集记录的是当前日期时间下,售货机所售卖商品的订单状况,其出货状态有出货成功、出货失败、未出货等多种情况。然而,为预测未来4周的销售额,其所需样本数据应为实际的周销售额数据,因此,需要筛选状态为出货成功的数据并统计各周销售额,如代码清单14所示。
代码清单14 筛选出货成功数据并统计各周销售额
| import pandas as pd import matplotlib.pyplot as plt from statsmodels.tsa.stattools import adfuller as ADF from statsmodels.graphics.tsaplots import plot_acf from statsmodels.stats.diagnostic import acorr_ljungbox from statsmodels.tsa.arima_model import ARIMA data = pd.read_csv('../tmp/order.csv', encoding='gbk') # 提取出货状态为“出货成功”的下单时间和总金额(元)数据 data_info = data.loc[data['出货状态'] == '出货成功', ['下单时间', '总金额(元)']] data_info = data_info.set_index('下单时间') # 将下单时间设为索引 # 将索引修改为日期时间格式 data_info.index = pd.to_datetime(data_info.index) # 按周对总金额进行汇总,即求和 data_w = data_info.resample('W').sum() |
2.平稳性检验
在使用ARIMA模型进行销售额预测之前,需要查看时间序列是否平稳,若数据非平稳,在数据分析挖掘的时候,则可能会产生“伪回归”等问题,从而影响分析结果。通过时间序列的时序图、自相关图及其单位根查看时间序列平稳性,时序图如图16所示,自相关图如图17所示,单位根检验结果如图18所示。

图16 原始序列的时序图

图17 原始序列的自相关图

图18 原始序列的单位根检验结果
由图16可知,时序图显示该序列具有明显的递增趋势,可以判断为原始序列数据是非平稳序列;图17的自相关图显示的自相关系数大部分均大于零,说明序列间具有一定的长期相关性。由图18可知,在单位根检验统计量中,p值为0.251134,其值显著大于0.05,可以推断出该序列为非平稳序列(非平稳序列一定不是白噪声序列)。
绘制时序图、自相关图并进行单位根检验如代码清单15所示。
代码清单15 绘制时序图、自相关图并进行单位根检验
| # 平稳性检验 # 判断是否为时间序列 plt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文标签 plt.rcParams['axes.unicode_minus'] = False # 显示负号 plt.figure(figsize=(8, 5)) plt.plot(data_w) plt.tick_params(labelsize=14) # 设置坐标轴字体大小 plt.show() # 定义绘制自相关图函数 def draw_acf(ts): plt.figure(facecolor='white', figsize=(10, 8)) plot_acf(ts) plt.show() # 定义单位根检验函数 def testStationarity(ts): dftest = ADF(ts) # 对ADF求得的值进行语义描述 dfoutput = pd.Series(dftest[0:4], index = ['Test Statistic','p-value','#Lags Used', 'Number of Observations Used']) for key, value in dftest[4].items(): dfoutput['Critical Value (%s)'%key] = value return dfoutput # 自相关 draw_acf(data_w) # 单位根检验 print('单位根检验结果为:\n', testStationarity(data_w)) |
3.差分处理
在进行平稳性检验后,发现原始序列数据属于非平稳序列,而在使用ARIMA模型进行销售额预测时,需要序列数据是平稳序列,以避免序列中的随机游走形势影响预测结果。在Python中,可以通过二阶差分处理对数据进行平稳化操作,并查看二阶差分之后序列的平稳性和白噪声,其中二阶差分后序列的时序图如图19所示,二阶差分后序列的自相关图如图20所示,二阶差分后序列的单位根检验结果如图21所示,二阶差分后序列的白噪声检验结果如图22所示。

图19 二阶差分后序列的时序图

图20 二阶差分后序列的自相关图

图21 二阶差分后序列的单位根检验结果
![]()
图22 二阶差分后序列的白噪声检验结果
由图19可知,该序列无明显趋势,较为稳定;图20的自相关图显示自相关系数较为均匀,且较为接近于0,有较强的短期相关性。由图21可知,二阶差分后序列的单位根检验p值远小于0.05,可以判断出差分处理后的序列是平稳序列。由图22可知,在白噪声检验结果中,输出的p值小于0.05,同时结合单位根检验结果可以判断二阶差分之后的序列是平稳非白噪声序列。
差分处理并查看序列平稳性和白噪声如代码清单16所示。
代码清单16 差分处理并查看序列平稳性和白噪声
| # 二阶差分处理 data_w_T1 = data_w.diff().dropna() data_w_T2 = data_w_T1.diff().dropna() # 差分后的时间序列图 plt.figure(figsize=(8, 5)) plt.plot(data_w_T2) plt.tick_params(labelsize=14) plt.show() # 差分自相关 draw_acf(data_w_T2) # 差分单位根检验 print('差分单位根检验结果为:\n', testStationarity(data_w_T2)) # 白噪声检验 print('差分白噪声检验结果为:\n', acorr_ljungbox(data_w_T2, lags=1)) |
4.模型定阶
通常情况下,在进行模型预测前,需要寻找最优模型,以提高预测结果的准确性。针对ARIMA模型,可以通过BIC矩阵进行模型定阶。由于4.4.3小节进行了二阶差分处理,所以d=2。通过计算ARIMA(p,2,q)中所有组合的BIC信息量,取最小BIC信息量所对应的模型阶数,进而确定p值和q值,结果如图23所示。
![]()
图23 模型定阶
由操作结果可知,当p值为0、q值为1时,BIC值最小,到此p、q定阶完成。
模型定阶如代码清单17所示。
代码清单17 模型定阶
| # 通过BIC矩阵进行模型定阶 data_w = data_w.astype(float) pmax = 3 qmax = 3 bic_matrix = [] # 初始化BIC矩阵 for p in range(pmax+1): tmp = [] for q in range(qmax+1): try: tmp.append(ARIMA(data_w, (p, 2, q)).fit().bic) except: tmp.append(None) bic_matrix.append(tmp) bic_matrix = pd.DataFrame(bic_matrix) # 找出最小值位置 p, q = bic_matrix.stack().idxmin() print('当BIC最小时,p值和q值分别为: ', p, q) |
5.模型预测
应用ARIMA(0, 2, 1)模型对未来4周内商品的销售额进行预测,结果如图24所示。

图24预测未来4周的销售额
预测未来4周内商品的销售额如代码清单18所示。
代码清单18 预测未来4周内商品的销售额
| # 构建ARIMA(0, 2, 1)模型 model = ARIMA(data_w, (p, 2, q)).fit() # 预测未来4周的销售额 print('预测未来4周的销售额,其预测结果、标准误差、置信区间如下。\n', model.forecast(4)) |
注:利用ARIMA模型向前预测的周期越长,其误差越大。
推荐阅读

正版链接:https://item.jd.com/13814157.html
《Python数据挖掘:入门、进阶与实用案例分析》是一本以项目实战案例为驱动的数据挖掘著作,它能帮助完全没有Python编程基础和数据挖掘基础的读者快速掌握Python数据挖掘的技术、流程与方法。在写作方式上,与传统的“理论与实践结合”的入门书不同,它以数据挖掘领域的知名赛事“泰迪杯”数据挖掘挑战赛(已举办10届)和“泰迪杯”数据分析技能赛(已举办5届)(累计1500余所高校的10余万师生参赛)为依托,精选了11个经典赛题,将Python编程知识、数据挖掘知识和行业知识三者融合,让读者在实践中快速掌握电商、教育、交通、传媒、电力、旅游、制造等7大行业的数据挖掘方法。
本书不仅适用于零基础的读者自学,还适用于教师教学,为了帮助读者更加高效地掌握本书的内容,本书提供了以下10项附加价值:
(1)建模平台:提供一站式大数据挖掘建模平台,免配置,包含大量案例工程,边练边学,告别纸上谈兵
(2)视频讲解:提供不少于600分钟Python编程和数据挖掘相关教学视频,边看边学,快速收获经验值
(3)精选习题:精心挑选不少于60道数据挖掘练习题,并提供详细解答,边学边练,检查知识盲区
(4)作者答疑:学习过程中有任何问题,通过“树洞”小程序,纸书拍照,一键发给作者,边问边学,事半功倍
(5)数据文件:提供各个案例配套的数据文件,与工程实践结合,开箱即用,增强实操性
(6)程序代码:提供书中代码的电子文件及相关工具的安装包,代码导入平台即可运行,学习效果立竿见影
(7)教学课件:提供配套的PPT课件,使用本书作为教材的老师可以申请,节省备课时间
(8)模型服务:提供不少于10个数据挖掘模型,模型提供完整的案例实现过程,助力提升数据挖掘实践能力
(9)教学平台:泰迪科技为本书提供的附加资源提供一站式数据化教学平台,附有详细操作指南,边看边学边练,节省时间
(10)就业推荐:提供大量就业推荐机会,与1500+企业合作,包含华为、京东、美的等知名企业
通过学习本书,读者可以理解数据挖掘的原理,迅速掌握大数据技术的相关操作,为后续数据分析、数据挖掘、深度学习的实践及竞赛打下良好的技术基础。

转载自:自动售货机销售数据分析与应用
- 本次送书三本
- 活动时间:截止到2023-10-22
- 参与方式:关注博主、并在此文章下面点赞、收藏并任意评论。



![y _hat[ [ 0, 1], y ]语法——pytorch张量花式索引](http://pic.xiahunao.cn/y _hat[ [ 0, 1], y ]语法——pytorch张量花式索引)



系统时钟)




)






