💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码、数据、文献
💥1 概述

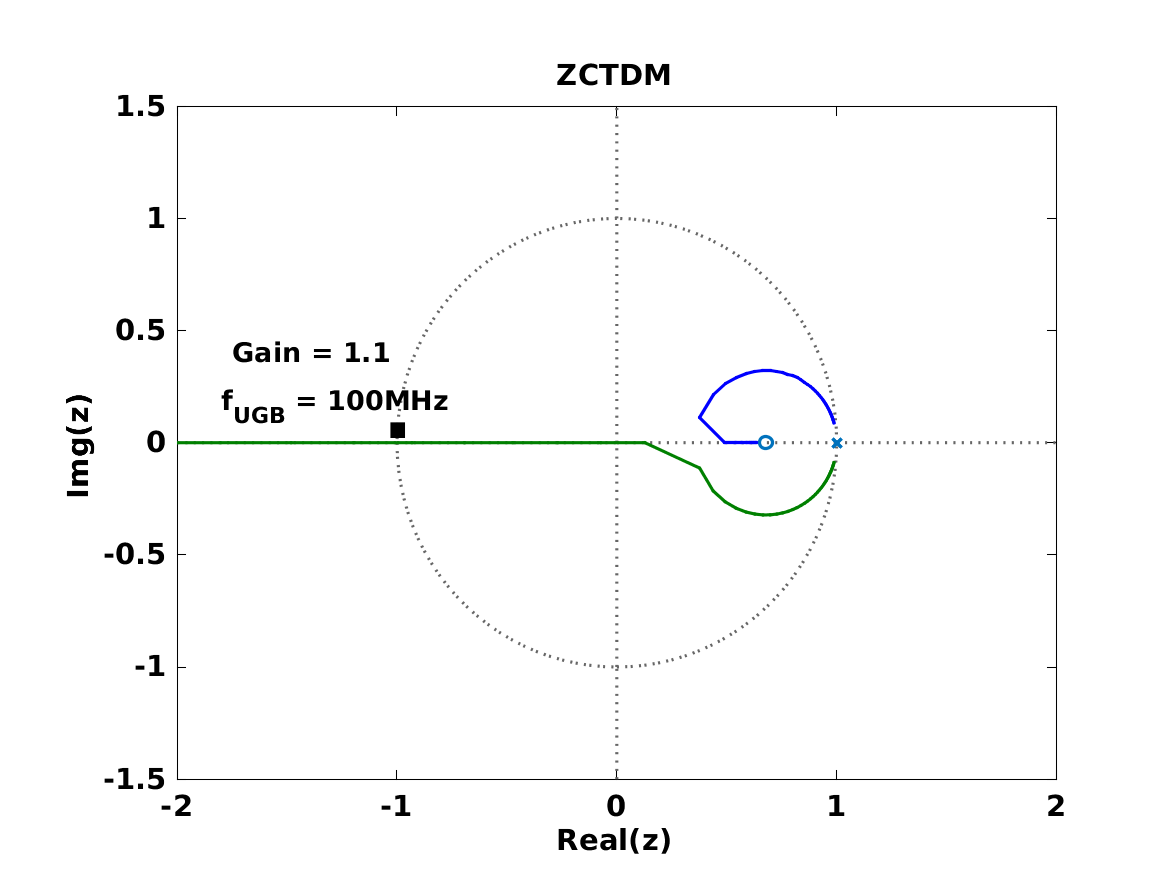
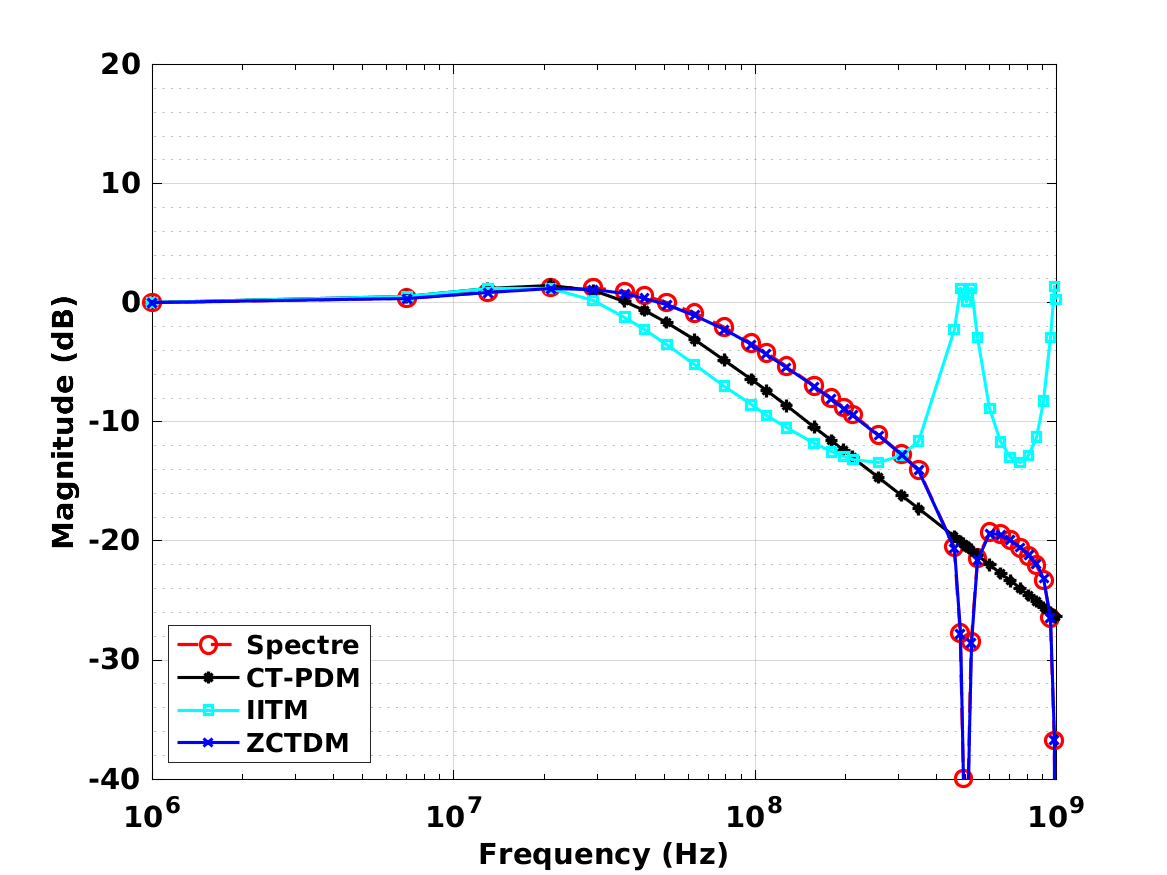
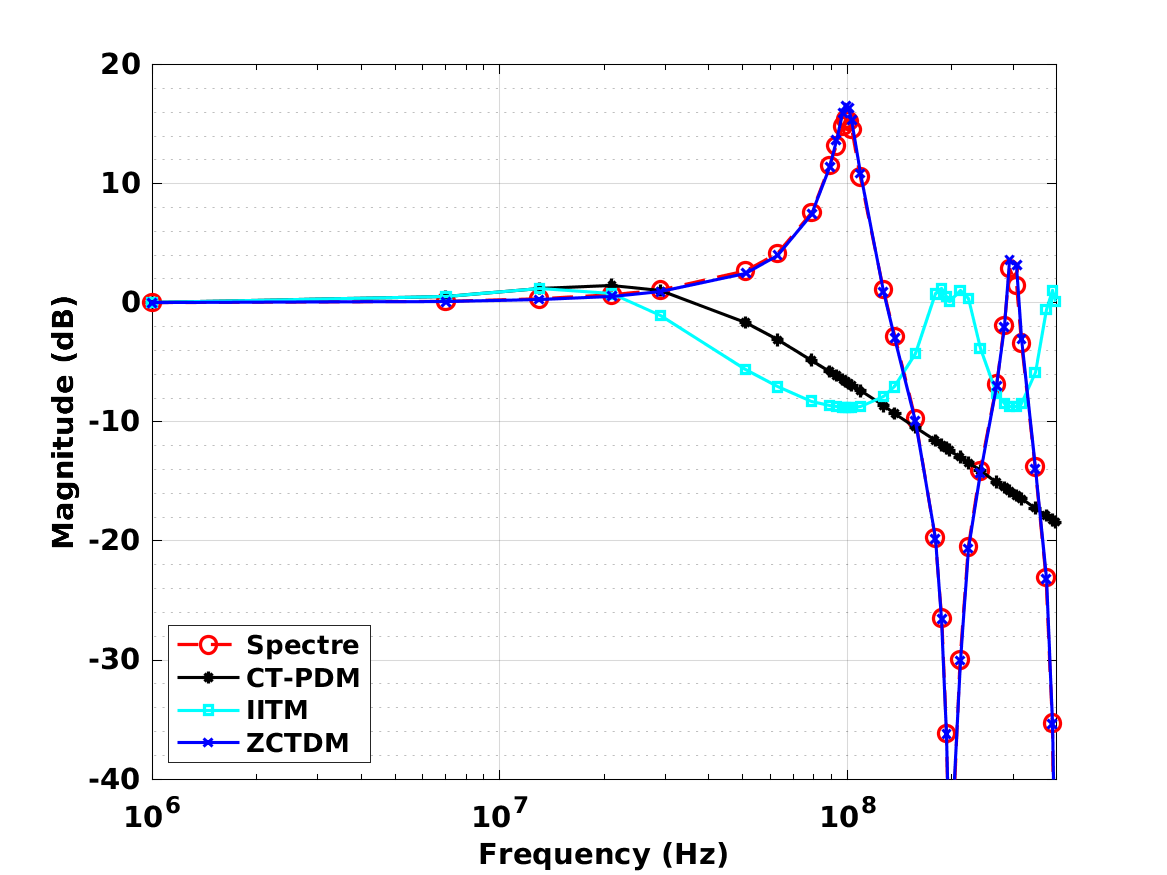
本文介绍了基于电压控制振荡器的跨导运算放大器(VCO-OTA)的过零时差模型(ZCTDM)。小信号、线性、离散时间模型以等距时间间隔提供输出电流脉冲,其幅度与VCO-OTA中两个VCO的过零点之间的时间差成正比。与连续时相域模型(CT-PDM)和脉冲不变变换模型(IITM)相比,ZCTDM考虑了VCO振荡频率附近输出端产生的高频信号和高频输入响应。因此,ZCTDM在反馈配置中捕获VCO-OTA的完整环路响应,只要输出电压放电速率小于系统更新速率,大多数应用中都是这种情况。通过两个设计示例演示了该模型的应用。使用ZCTDM建模的系统的频率响应与使用广泛的行为模型模拟的响应的频率响应在0.5dBRMS以内,而使用CT-PDM和IITM得出的结果在定性和定量上都存在显着偏差。
操作跨导放大器(OTA)构成了许多模拟和混合信号电路的核心,例如滤波器、RF调制器、DC-DC转换器和模数转换器(ADC)[1]–[6]。随着过去几十年技术的发展,晶体管的电源电压和固有增益降低了,而晶体管速度却提高了[7]。对于模拟电路,尤其是OTA,需要晶体管的高固有增益才能提供高直流增益。随着电源电压的缩放,晶体管的堆叠变得越来越困难,因此必须使用多级OTA来提供高直流增益。然而,在此类 OTA 中,在保持稳定性的同时实现高带宽变得困难。
基于压控振荡器 (VCO) 的 OTA (VCO-OTA) [图 1(a)] 已成为传统放大器的替代品,并且由于频率到相位转换而提供高直流增益。他们受益于技术扩展,因为他们的块[1]-[3],[8]-[10]的数字性质。VCO-OTA已在滤波器、接收器、DC-DC转换器、低压差稳压器和ADC [1]–[6]、[8]–[14]等多种应用中得到证明。
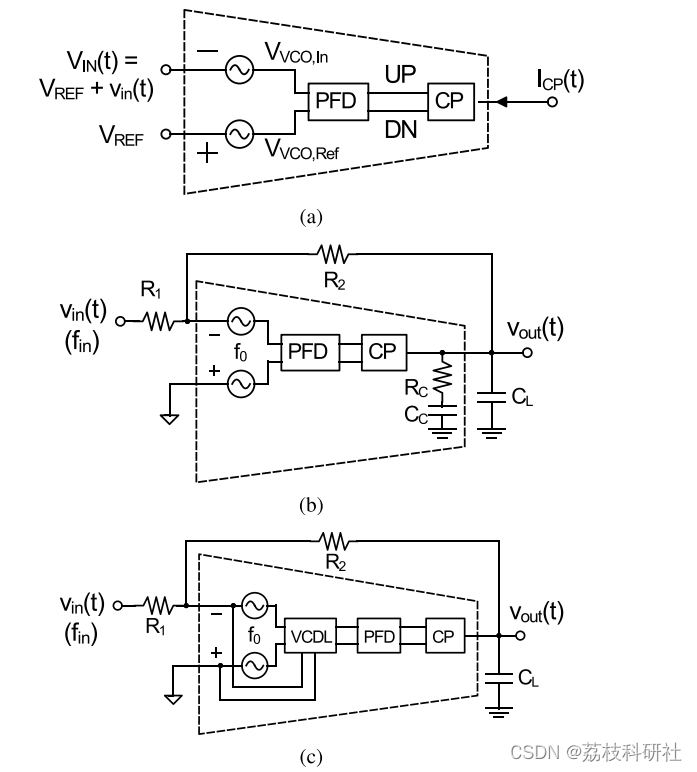
📚2 运行结果
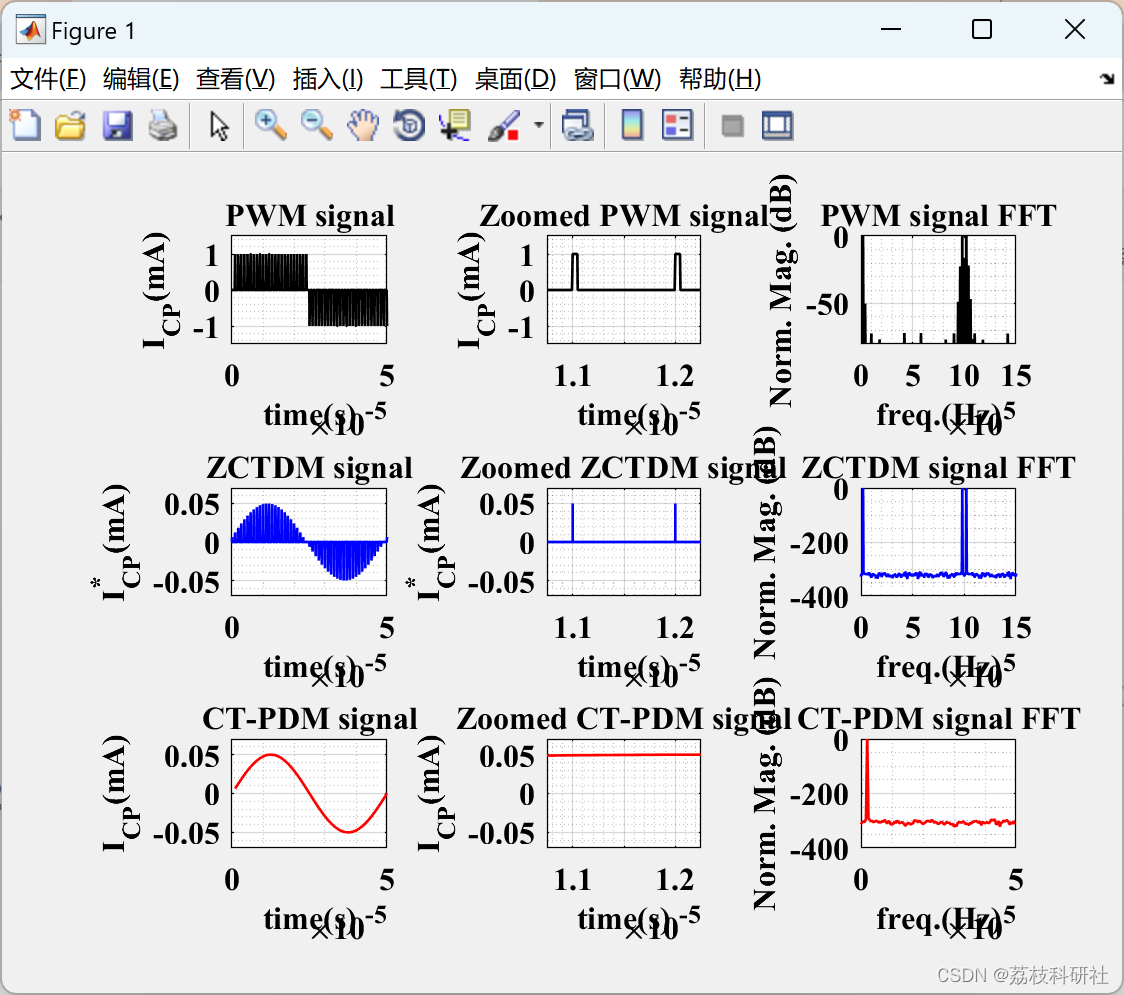
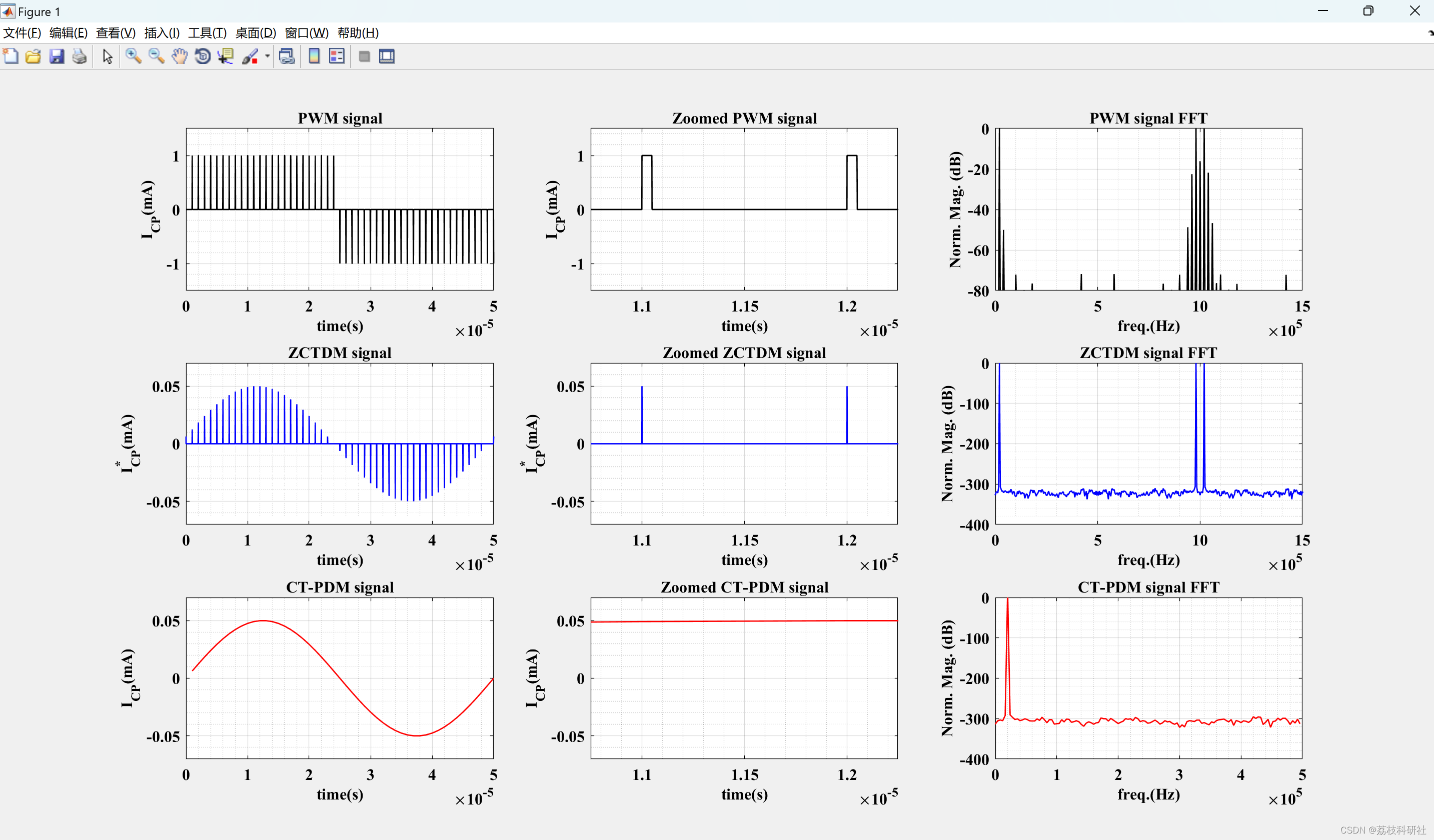
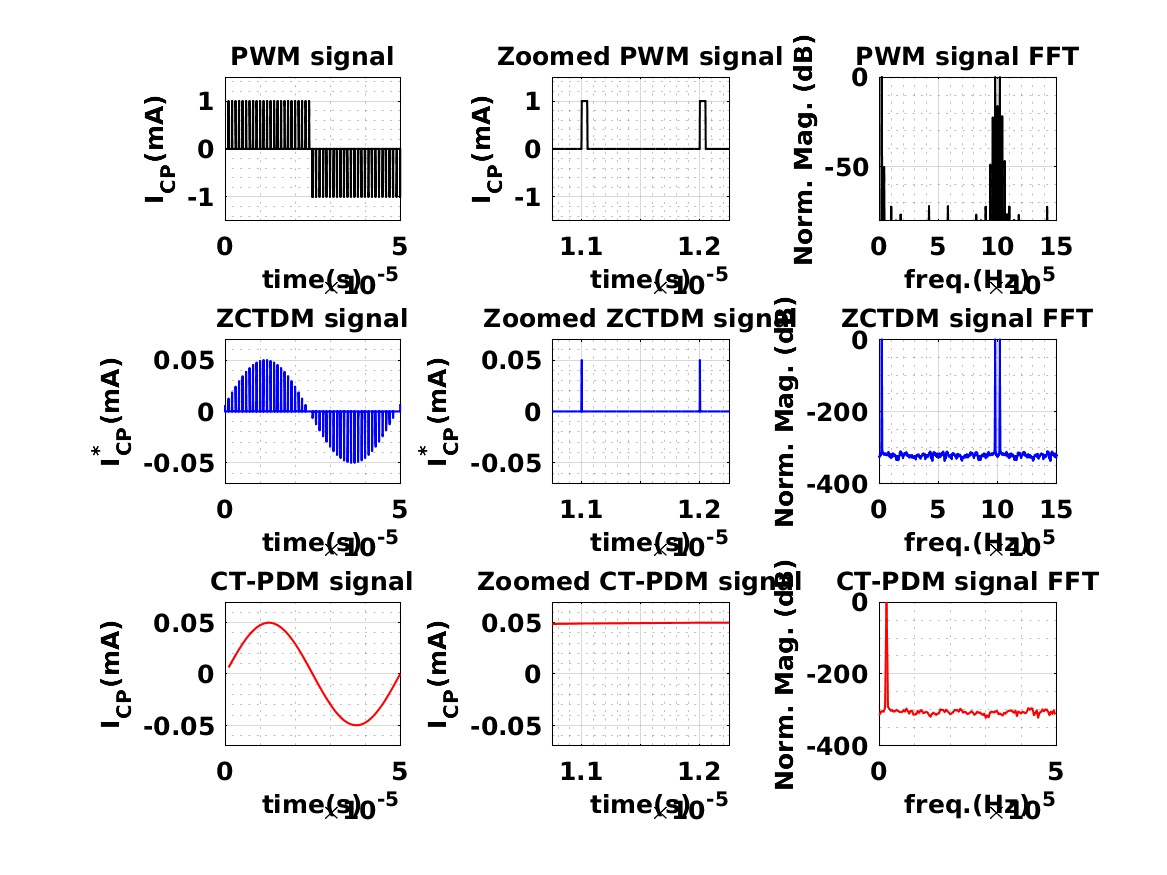
剩余其他运行结果图直接去掉Matlab外框 。
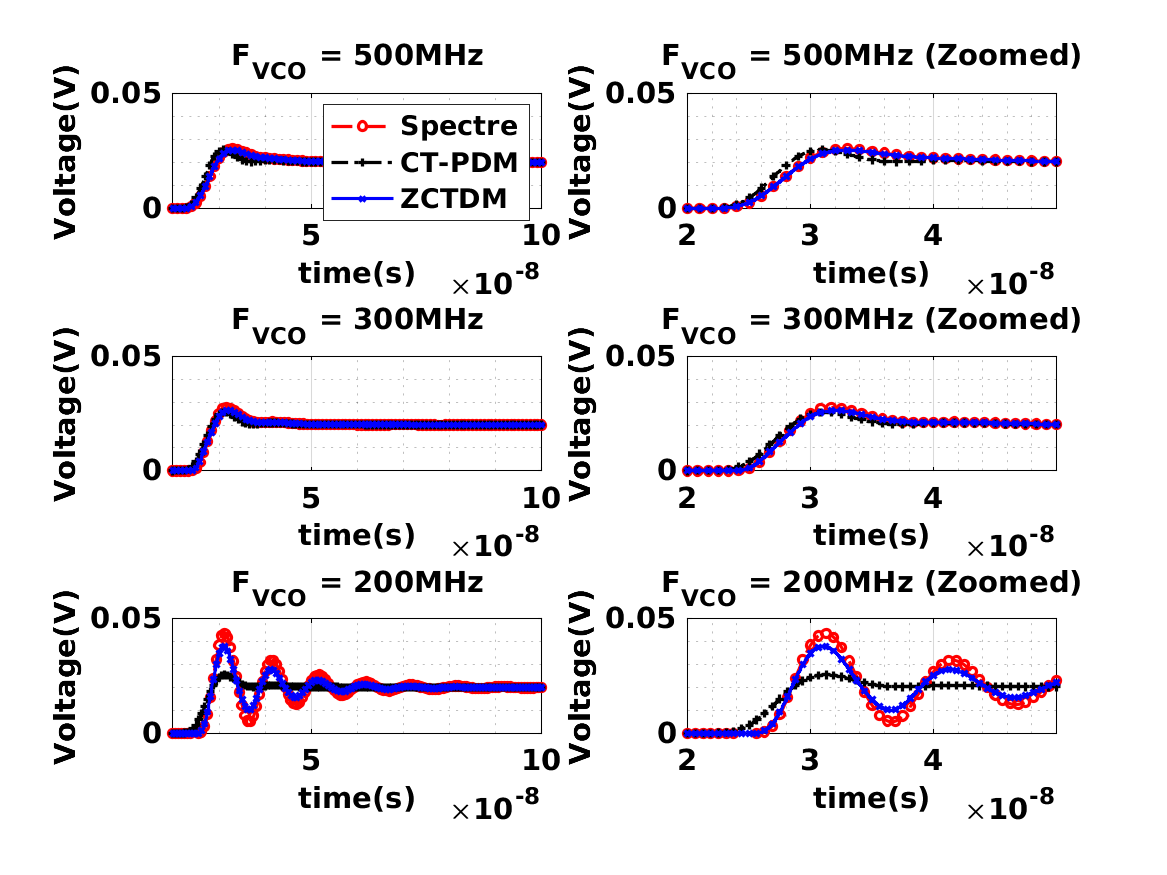
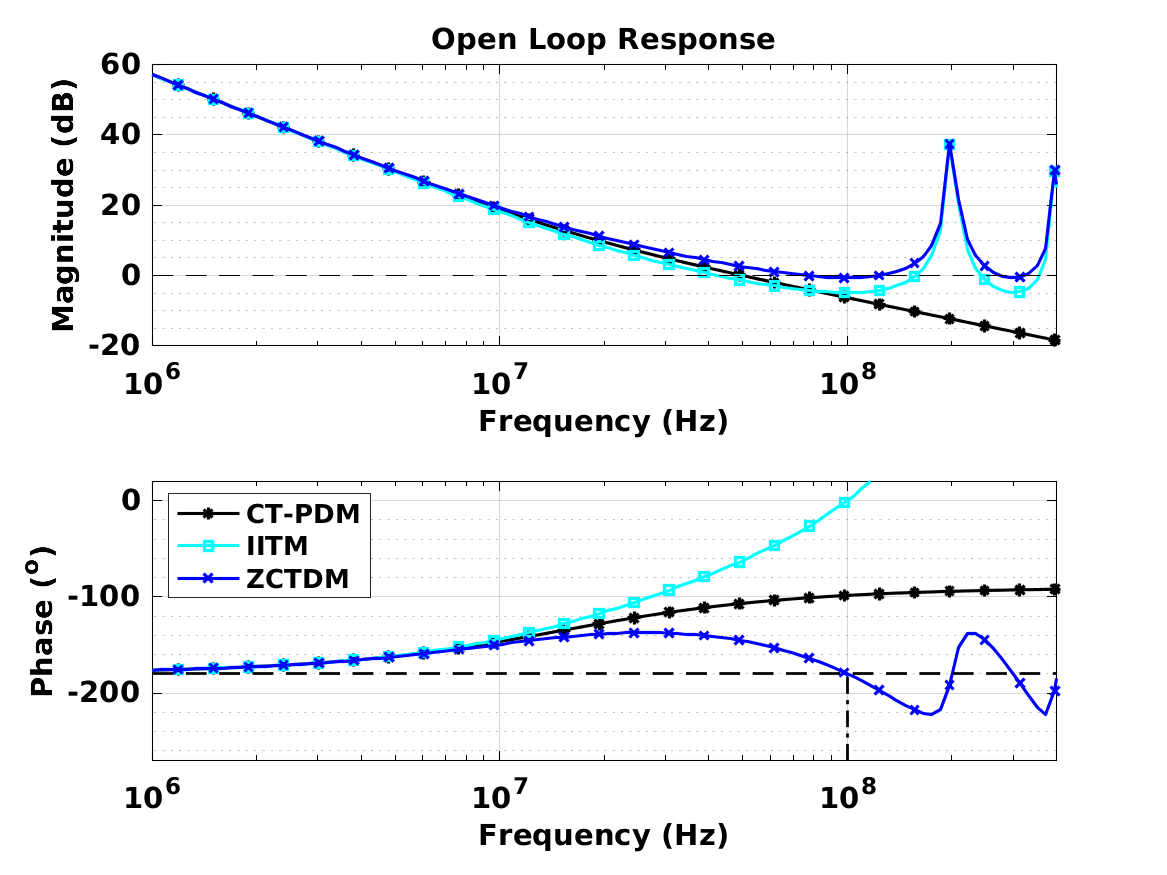
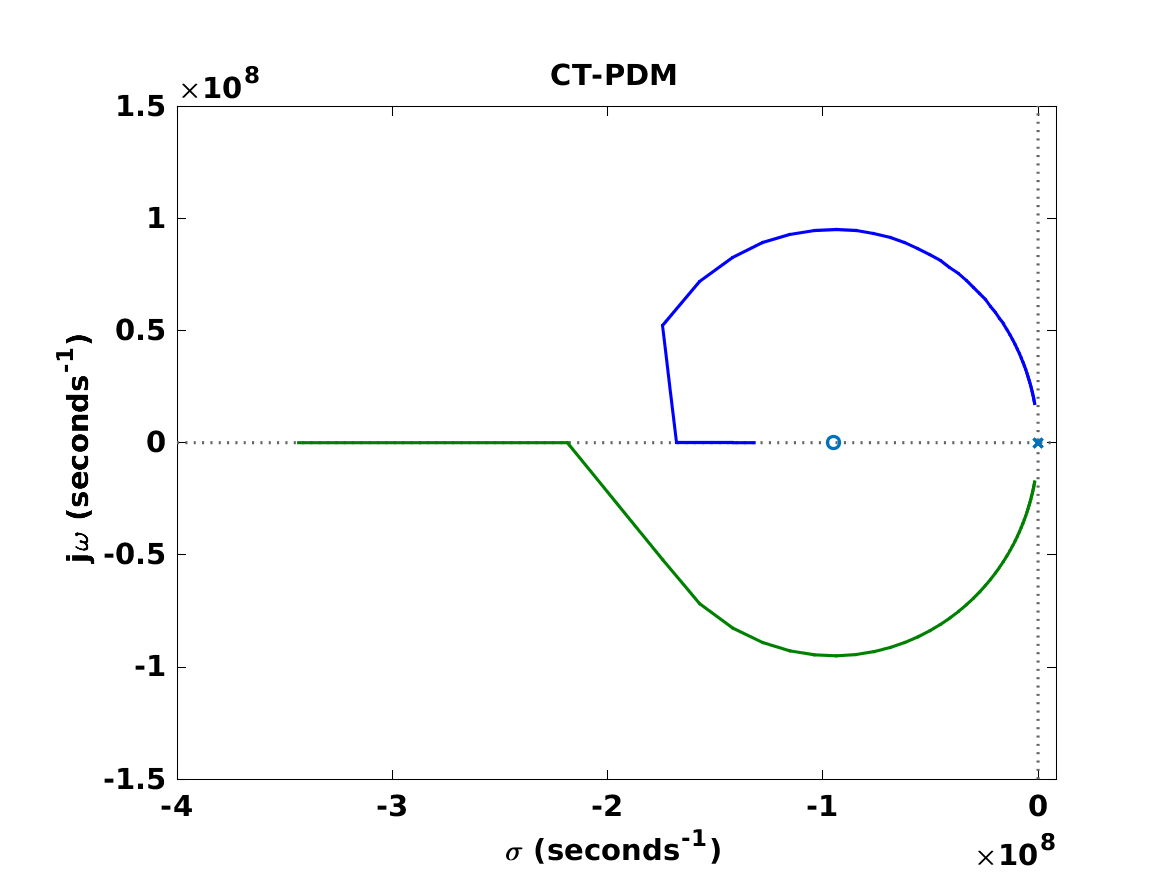
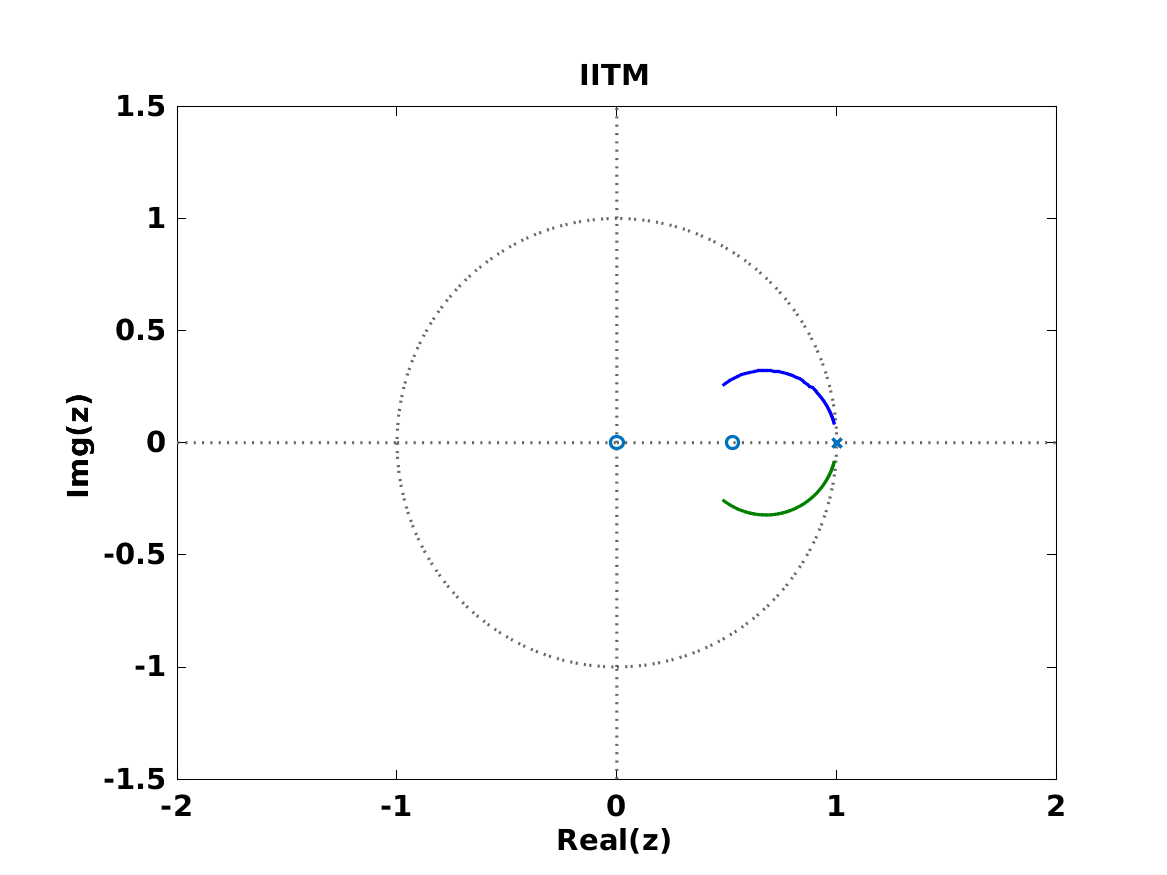


部分代码:
%% Plots:
% first row: simple sine wave sampled at vco frequency and its spectrum
% second row: emulates impulses. So the spectrum contains first order
% tones.
% third row: creating PWM and plotting that.
figure(1); clf;
subplot(3,3,1)
plot((1:length(vin_pwm))*ts,vin_pwm,'-k','LineWidth',line_width); grid on; ylim([-1.5*PWM_amp_max,1.5*PWM_amp_max]); xlim([0,1/fin]);
subplot(3,3,3);
plot(1/(tsim)*(-length(vin_pwm)/2:length(vin_pwm)/2-1),pwm_fft_norm,'-k', 'LineWidth',line_width); grid on; xlim([0,1.5/tvco]); ylim([-80, 0]);
subplot(3,3,4);
plot((1:length(vin_upsampled))*ts,vin_upsampled,'-b', 'LineWidth',line_width); grid on; xlim([0,1/fin]); ylim([-1.4*A,1.4*A]);
subplot(3,3,6);
plot(1/(tsim)*(-length(vin_upsampled)/2:length(vin_upsampled)/2-1),upsampled_fft_norm,'-b', 'LineWidth',line_width); grid on; xlim([0,1.5/tvco]);
subplot(3,3,7);
plot((1:length(vin))*ts*OSR,vin,'-r', 'LineWidth',line_width); grid on; xlim([0,1/fin]);ylim([-1.4*A,1.4*A]);
subplot(3,3,9);
plot(1/tsim*(-length(vin)/2:length(vin)/2-1),20*log10(fftshift(abs(fft(vin)))),'-r', 'LineWidth',line_width); grid on; xlim([0,0.5/tvco]); ylim([-400,0]);
subplot(3,3,1); fig_set_text('PWM signal', 'time(s)','I_{CP}(mA)',font_size);
subplot(3,3,3); fig_set_text('PWM signal FFT', 'freq.(Hz)','Norm. Mag. (dB)',font_size);
subplot(3,3,4); fig_set_text('ZCTDM signal', 'time(s)','I_{CP}^*(mA)',font_size);
subplot(3,3,6); fig_set_text('ZCTDM signal FFT', 'freq.(Hz)','Norm. Mag. (dB)',font_size);
% s_ylabel = '$$\overline{I_{CP}}$$(mA)';
s_ylabel = 'I_{CP}(mA)';
subplot(3,3,7); fig_set_text('CT-PDM signal', 'time(s)',s_ylabel,font_size);
% h = ylabel(s_ylabel,'FontName','Times','fontweight','bold','fontsize',fontsize,'Interpreter','latex');
subplot(3,3,9); fig_set_text('CT-PDM signal FFT', 'freq.(Hz)','Norm. Mag. (dB)',font_size);
subplot(3,3,2);
plot((1:length(vin_pwm))*ts,vin_pwm,'-k','LineWidth',line_width); grid on; ylim([-1.5*PWM_amp_max,1.5*PWM_amp_max]); xlim([0.215/fin,0.245/fin]);
subplot(3,3,5);
plot((1:length(vin_upsampled))*ts,vin_upsampled,'-b', 'LineWidth',line_width); grid on; xlim([0.215/fin,0.245/fin]); ylim([-1.4*A,1.4*A]);
subplot(3,3,8);
plot((1:length(vin))*ts*OSR,vin,'-r', 'LineWidth',line_width); grid on; xlim([0.215/fin,0.245/fin]);ylim([-1.4*A,1.4*A]);
subplot(3,3,2); fig_set_text('Zoomed PWM signal', 'time(s)','I_{CP}(mA)',font_size);
subplot(3,3,5); fig_set_text('Zoomed ZCTDM signal', 'time(s)','I_{CP}^*(mA)',font_size);
subplot(3,3,8); fig_set_text('Zoomed CT-PDM signal', 'time(s)',s_ylabel,font_size);
saveas(gcf, '../results/Fig05.png');
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。


)







简明教程)
)









