2.1简介

多臂老虎机问题可以被看作简化版的强化学习问题。但是其只有动作和奖励没有状态信息，算是简化版的强化学习问题。

2.2问题介绍

2.2.1问题定义

在多臂老虎机(MAB)问题中，有一个有K根拉杆的老虎机，拉动每一根拉杆都对应一个关于奖励的概率分布$R$。我们每次拉动其中一根拉杆，就可以从该拉杆对应的奖励概率分布中获得一个奖励$r$。
我们在各个拉杆的奖励概率分布未知的情况下，从头尝试，目标是操作T次拉杆后获得尽可能高的累积奖励。
由于奖励的概率分布是未知的，所以我们需要在探索拉杆的获奖概率和根据经验选择获奖最多的拉杆中进行权衡。采用怎样的操作策略才能使获得的累积奖励最高便是多臂老虎机问题。

2.2.2形式化描述

多臂老虎机问题可以表示为一个元组$<A,R>$，其中：

• A为动作集合，其中一个动作表示拉动一个拉杆。若多臂老虎机一共有K根拉杆，那动作空间就是集合，我们用$a_t\in A$表示任意一个动作
• R为奖励概率分布，拉动每一根拉杆的动作a都对应一个奖励概率分布R(r|a)，不同拉杆的奖励分布通常是不同的。
  假设每个时间步只能拉动一个拉杆，多臂老虎机的目标为最大化一段时间步T内累积的奖励：$max\sum _{t=1}^T{r}_t,r_t\sim R(\cdot |a_t)$，其中$a_t$表示在第t时间步拉动某一拉杆的动作，$r_t$表示动作$a_t$获得的奖励。

在 $r_t\sim R(\cdot |a_t)$ 中，符号 $\cdot$ 表示一个占位符，通常用来表示条件概率的输入或条件。在这个上下文中，它表示奖励 $r_t$ 是从奖励分布 R 中根据条件 $a_t$ 抽取的。也就是说，它指代了在给定动作 $a_t$ 的条件下，奖励 $r_t$ 的分布。
这种表示方法用于表达随机性和条件性概率分布，它告诉我们奖励 $r_t$ 是依赖于代理选择的动作 $a_t$ 而发生的，不同的动作可能导致不同的奖励分布。这对于解释多臂老虎机问题中的随机性和条件性关系非常有用。

2.2.3累积懊悔

对于每一个动作a，我们定义其期望奖励为$Q(a)={\mathbb{E}}_{r\sim R(\cdot |a)}[r]$，于是，至少存在一根拉杆，它的期望奖励不小于拉动其他任意一根拉杆，我们将该最优期望奖励表示为$Q^{\ast }=ma{x}_{a\in A}Q(a)$。为了更加直观、方便地观察拉动一根拉杆的期望奖励离最优拉杆期望奖励的差距，我们引入懊悔(regret)概念。
懊悔定义为拉动当前拉杆的动作a与最优拉杆的期望奖励差，即$R(a)=Q^{\ast }-Q(a)$。
累积懊悔(cumulative regret)即操作T次拉杆后累积的懊悔总量，对于一次完整的T步决策 { a 1 , a 2 , . . . , a T } \{a_1,a_2,...,a_T\} {a1​,a2​,...,aT​}，累积懊悔为${\sigma }_R=\sum _{t=1}^{T}R(a_t)$，MAB问题的目标为最大化累积奖励，等价于最小化累积懊悔。

符号 $\mathbb{E}$ 表示数学期望（Expectation），而不带修饰的 “E” 通常用于表示一般的期望值。它们之间的区别在于：

1. $\mathbb{E}$：这是一种数学符号，通常用于表示数学期望操作。在LaTeX等数学标记系统中，$\mathbb{E}$通常用于表示数学期望，表示对随机变量的期望值。数学期望是一个用于描述随机变量平均值的概念。通常，数学期望表示为：
   $$\mathbb{E}[X]$$
   其中，X 是随机变量，$\mathbb{E}[X]$ 表示随机变量 X 的期望值。
2. E：这是字母 “E” 的一般表示，可能用于表示其他数学或物理概念中的变量或符号，不一定表示数学期望。如果没有明确的上下文或标记，它可能表示其他概念，而不是期望操作。

所以，$\mathbb{E}$ 是专门用于表示数学期望的符号，而 “E” 可能用于其他用途。当你看到 $\mathbb{E}[X]$，它明确表示对随机变量 X 的数学期望，而 “E” 会根据上下文的不同而有不同的含义。

$Q(a)={\mathbb{E}}_{r\sim R(\cdot |a)}[r]$这个方程表示了动作值函数 Q(a) 的定义，其中 Q(a) 表示对动作 a 的期望奖励值。让我来解释它：

• $Q(a)$：这是动作值函数，表示选择动作 a 后的期望奖励值。动作值函数告诉代理在选择特定动作 a 时，可以预期获得多少奖励。
• ${\mathbb{E}}_{r\sim R(\cdot |a)}[r]$：这是期望操作，表示对随机变量 r 的期望，其中 r 来自奖励分布 R(·|a)。这个期望操作告诉我们，在给定动作 a 的情况下，随机抽取的奖励 r 的期望值。

具体来说，$Q(a)$ 是在选择动作 a 后，从奖励分布 R(·|a) 中随机抽取奖励 r 并计算其期望值的结果。这是一种在强化学习中用于估计动作的价值的常见方法。代理使用动作值函数来指导其决策，选择具有最高动作值的动作，以最大化累积奖励。

2.2.4估计期望奖励

为了知道拉动哪一根拉杆能获得更高的奖励，我们需要估计拉动这跟拉杆的期望奖励。由于只拉动一次拉杆获得的奖励存在随机性，所以需要多次拉动一根拉杆，然后计算得到的多次奖励的期望，其算法流程如下所示。

• 对与$\forall a\in A$，初始化计数器$N(a)=0$和期望奖励估值$\hat{Q}(a)=0$
• for $t=1\to T$do
  • 选取某根拉杆，该动作记为$a_t$
  • 得到奖励$r_t$
  • 更新计数器：$N(a_t)=N(a_t)+1$
  • 更新期望奖励估值：$\hat{Q}(a_t)=\hat{Q}(a_t)+\frac{1}{N(a_t)}[r_t-\hat{Q}(a_t)]$
• end for
  以上for循环中的第四步如此更新估值，是因为这样可以进行增量式的期望更新，公式如下。
  $$Q_k=\frac{1}{k}\sum _{i=1}^k{r}_i=$$
  
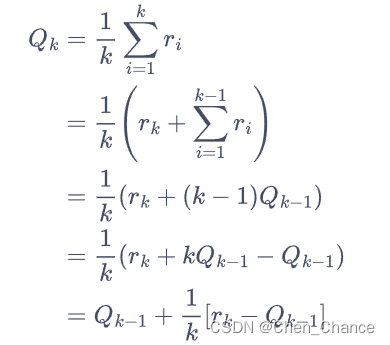
  如果将所有数求和再除以次数，其缺点是每次更新的时间复杂度和空间复杂度均为$O(n)$。而采用增量式更新，时间复杂度和空间复杂度均为$O(1)$

下面我们编写代码来实现一个拉杆数为 10 的多臂老虎机。其中拉动每根拉杆的奖励服从伯努利分布（Bernoulli distribution），即每次拉下拉杆有p的概率获得的奖励为 1，有1-p的概率获得的奖励为 0。奖励为 1 代表获奖，奖励为 0 代表没有获奖。

# 导入需要使用的库,其中numpy是支持数组和矩阵运算的科学计算库,而matplotlib是绘图库
import numpy as np
import matplotlib.pyplot as pltclass BernoulliBandit:""" 伯努利多臂老虎机,输入K表示拉杆个数 """def __init__(self, K):self.probs = np.random.uniform(size=K)  # 随机生成K个0～1的数,作为拉动每根拉杆的获奖概率self.best_idx = np.argmax(self.probs)  # 获奖概率最大的拉杆self.best_prob = self.probs[self.best_idx]  # 最大的获奖概率self.K = Kdef step(self, k):# 当玩家选择了k号拉杆后,根据拉动该老虎机的k号拉杆获得奖励的概率返回1（获奖）或0（未# 获奖）if np.random.rand() < self.probs[k]:return 1else:return 0np.random.seed(1)  # 设定随机种子,使实验具有可重复性
K = 10
bandit_10_arm = BernoulliBandit(K)
print("随机生成了一个%d臂伯努利老虎机" % K)
print("获奖概率最大的拉杆为%d号,其获奖概率为%.4f" %(bandit_10_arm.best_idx, bandit_10_arm.best_prob))

随机生成了一个10臂伯努利老虎机
获奖概率最大的拉杆为1号,其获奖概率为0.7203