20. 有效的括号

难度：easy

类型：栈与队列

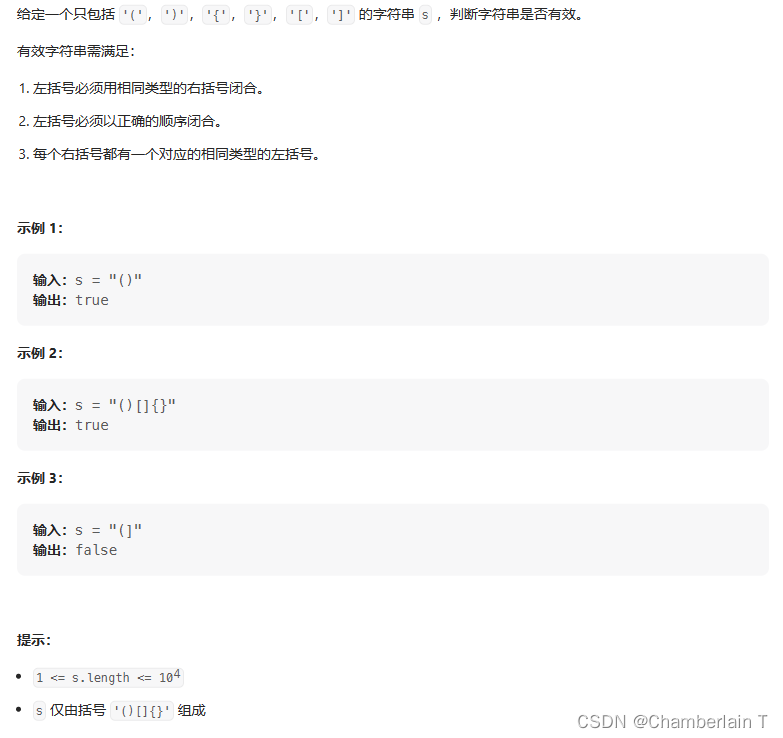
思路：

利用栈来做括号匹配；

代码：

class Solution {public boolean isValid(String s) {Deque<Character> stack = new ArrayDeque<>();for (int i = 0; i < s.length(); i++) {char c = s.charAt(i);if (c == '(' || c == '[' || c == '{') {// 将左括号入栈stack.push(c);} else if (!stack.isEmpty() && stack.peek() == leftOf(c)) {// 栈不为空，并且右括号和栈顶元素匹配时，栈顶元素出栈stack.pop();} else {// 当出现右括号并且栈为空时，括号无效；或者栈不为空，右括号不匹配，括号无效return false;}}return stack.isEmpty();}// 返回右括号对应的左括号public char leftOf(char c) {if (c == ')') {return '(';} else if (c == ']') {return '[';} else if (c == '}') {return '{';}return 'f';}
}

复杂度分析：

时间复杂度: O(n)
空间复杂度: O(n)

1047. 删除字符串中的所有相邻重复项

难度：easy

类型：栈与队列

思路：

用栈来消去重复元素，当新元素与栈顶元素相同时，则pop；反之则push；需要注意的是，将栈中的元素拼接成字符串时，要注意元素顺序。

代码：

class Solution {public String removeDuplicates(String s) {Deque<Character> stack = new ArrayDeque<>();        for (int i = 0; i < s.length(); i++) {char c = s.charAt(i);if (stack.isEmpty() || c != stack.peek()) {stack.push(c);} else if (c == stack.peek()) {stack.pop();}}// 1.利用StringBuilder的insert方法// StringBuilder sb = new StringBuilder();// while (!stack.isEmpty()) {//     sb.insert(0, stack.pop());// }// return sb.toString();// 2.利用DequeString str = "";while (!stack.isEmpty()) {str += stack.pollLast();}return str;}
}

复杂度分析：

时间复杂度: O(n)
空间复杂度: O(n)

150. 逆波兰表达式求值

难度：，medium

类型：栈与队列

思路：

逆波兰表达式也叫后缀表达式（后序遍历），用它来处理算数表达式不需要考虑优先级；

遇到数字则入栈，遇到运算符则将两个元素出栈进行运算（注意两个元素的出栈顺序和计算顺序，例如除法运算中，先出栈的元素为除数，后出战的元素为被除数，被除数/除数），再将运算结果入栈。

代码：

class Solution {public int evalRPN(String[] tokens) {Deque<Integer> stack = new ArrayDeque<>();for (int i = 0; i < tokens.length; i++) {// 字符串对比内容使用equals方法，对比引用地址使用==，对象的赋值是改变引用if (tokens[i].equals("+")) {int a = stack.pop();int b = stack.pop();// b在前，a在后，因为栈是先进后出stack.push(b + a);} else if (tokens[i].equals("-")) {int a = stack.pop();int b = stack.pop();stack.push(b - a);} else if (tokens[i].equals("*")) {int a = stack.pop();int b = stack.pop();stack.push(b * a);} else if (tokens[i].equals("/")) {int a = stack.pop();int b = stack.pop();stack.push(b / a);} else {stack.push(Integer.valueOf(tokens[i]));}}return stack.pop();}
}

复杂度分析：