B-树:大数据
现代电子计算机发展速度空前,就存储能力而言,情况似乎也是如此:如今容量以TB计的硬盘也不过数百元,内存的常规容量也已达到GB量级。
然而从实际应用的需求来看,问题规模的膨胀却远远快于存储能力的增长。
在同等成本下,存储器的容量越大(小)则访问速度越慢(快)。
实践证明,分级存储是行之有效的方法。在由内存与外存(磁盘)组成的二级存储系统中,数据全集往往存放于外存中,计算过程中则可将内存作为外存的高速缓存,存放最常用数据项的复本。借助高效的调度算法,如此便可将内存的“高速度”与外存的“大容量”结合起来。
两个相邻存储级别之间的数据传输,统称I/O操作。(各级存储器的访问速度相差悬殊,故应尽可能地减少I/O操作)
以内存与磁盘为例,其单次访问延迟大致分别在纳秒(ns)和毫秒(ms)级别,相差5至6个数量级。对内存而言的一秒/一天,相当于磁盘的一星期/两千年。
多路搜索树(二叉搜索树与四路搜索树):将通常的二叉搜索树,改造为多路搜索树——在中序遍历的意义下,这也是一种等价变换。
 以两层为间隔,将各节点与其左、右孩子合并为“大节点”:原节点及其孩子的共三个关键码予以保留;孩子节点原有的四个分支也予以保留并按中序遍历次序排列;节点到左、右孩子的分支转化为“大节点”内部的搜索,在图中表示为水平分支。如此改造之后,每个“大节点”拥有四个分支,故称作四路搜索树。
以两层为间隔,将各节点与其左、右孩子合并为“大节点”:原节点及其孩子的共三个关键码予以保留;孩子节点原有的四个分支也予以保留并按中序遍历次序排列;节点到左、右孩子的分支转化为“大节点”内部的搜索,在图中表示为水平分支。如此改造之后,每个“大节点”拥有四个分支,故称作四路搜索树。
B-树:结构
所谓 m m m 阶 B-树,即 m m m 路平衡搜索树( m ≥ 2 m \geq 2 m≥2)
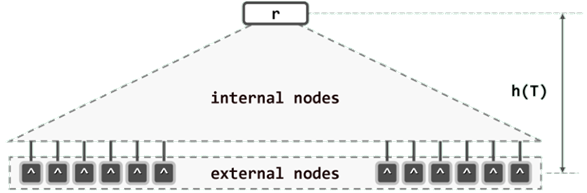
所有外部节点的深度统一相等。同时,每个内部节点都存有不超过m - 1个关键码,以及用以指示对应分支的不超过 m 个引用。
具体地,存有 n ≤ m − 1 n \leq m - 1 n≤m−1 个关键码: K 1 < K 2 < K 3 < K 4 < . . . < K n K_1 < K_2 <K_3 < K_4 < ... < K_n K1<K2<K3<K4<...<Kn 的内部节点,同时还配有 n + 1 ≤ m n+1 \leq m n+1≤m 个引用: A 0 < A 1 < A 2 < A 3 < A 4 < . . . < A n A_0 < A_1 <A_2<A_3 < A_4 <...<A_n A0<A1<A2<A3<A4<...<An。
反过来,各内部节点的分支数也不能太少。具体地,除根以外的所有内部节点,都应满足: n + 1 ≥ [ m / 2 ] n+1 \geq [m /2] n+1≥[m/2],而在非空的 B-树中,根节点应满足: n + 1 ≥ 2 n+1 \geq 2 n+1≥2。
由于各节点的分支数介于 [ m / 2 ] [m/2] [m/2] 至 m m m 之间,故 m m m 阶B-树也称作 ( m / 2 m/2 m/2, m)-树。
所有叶节点的深度统一相等。
计算B-树高度时,还需要计入其最底层的外部节点:树高 h = 外部节点的深度
实现
B-树节点
#include "../vector/vector.h"
#define BTNodePosi(T) BTNode<T>* //B-树节点位置template <typename T> struct BTNode { //B-树节点模板类
// 成员(为简化描述起见统一开放,读者可根据需要迕一步封装)BTNodePosi(T) parent; //父节点Vector<T> key; //关键码向量Vector<BTNodePosi(T)> child; //孩子向量(其长度总比key多一)
// 构造函数(注意:BTNode叧能作为根节点创建,而且初始时有0个关键码和1个空孩子指针)BTNode() { parent = NULL; child.insert ( 0, NULL ); }BTNode ( T e, BTNodePosi(T) lc = NULL, BTNodePosi(T) rc = NULL ) {parent = NULL; //作为根节点,而且初始时key.insert ( 0, e ); //叧有一个关键码,以及child.insert ( 0, lc ); child.insert ( 1, rc ); //两个孩子if ( lc ) lc->parent = this; if ( rc ) rc->parent = this;}
};
B-树
#include“BTNode.h” //引入B-树节点类template <typename T> class BTree [ //B-树模板类
protected:int _size;//存放的关键码总数int _order; //B-树的阶次,至少为3--创建时指定,一般不能修改BTNodePosi(T)_root; //根节点BTNodePosi(T)_hot; //BTree::search()最后访问的非空( 除非树空)的节点位置void solveOverflow ( BTNodePosi(T) ); //因插入而上溢之后的分裂处理void solveUnderflow ( BTNodePosi(T) ); //因删除而下溢之后的合并处理
public:BTree ( int order = 3 ): _order ( order ),_size ( ) //构造函数:默认为最低的3阶{_root = new BTNode<T>();}~BTree(){ if ( _root ) release ( _root );} //析构函数:释放所有节点int const order(){ return _order; } //阶次int const size(){ return _size; } //规模BTNodePosi(T) & root() { return_root;} //树根bool empty() const { return !_root;} //判空BTNodePosi(T) search ( const T& e ); //查找bool insert ( const T& e ); //插入bool remove ( const T& e ); //删除
}; //BTree
B-树:查找
只载入必需的节点,尽可能减少 I/O 操作。

可以将大数据集组织为 B-树并存放于外存。对于活跃的B-树,其根节点会常驻于内存;此外,任何时刻通常只有另一节点(称作当前节点)留驻于内存。
过程:
先以根节点作为当前节点,然后再逐层深入。若在当前节点(所包含的一组关键码)中能够找到目标关键码,则成功返回。否则(在当前节点中查找“失败”),则必可在当前节点中确定某一个引用(“失败”位置),并通过它转至逻辑上处于下一层的另一节点。若该节点不是外部节点,则将其载入内存,并更新为当前节点,然后继续重复上述过程。
实现
template<typename T> BTNodePosi(T) BTree<T>::search ( const T& e ) //在B-树中查找关键码eBTNodePosi(T) v =_root; _hot = NULL; //从根节点出发while ( v ){ //逐层查找Rank r = v->key.search ( e ); //在当前节点中,找到不大于e的最大关键码if ( ( 0 <= r ) && ( e == v->key[r] ) ) return v; //成功:在当前节点中命中目标关键码_hot = v; v = v->hild[r + 1]; //否则,转入对应子树(_hot指向其父)--需做I/0,最费时间}//这里在向量内是二分查找,但对通常的_order可直接顺序查找return NULL; //失败:最终抵达外部节点
}
成功时返回目标关键码所在的节点,上层调用过程可在该节点内进一步查找以确定准确的命中位置;失败时返回对应外部节点,其父节点则由变量_hot指代。
性能分析
B-树查找操作所需的时间消耗于两个方面:1.将某一节点载入内存;2.在内存中对当前节点进行查找。
对于高度为h的B-树,外存访问不超过O(h - 1)次.
若存有N个关键码的m阶B-树高度为h,则必有: log m ( N + 1 ) ≤ h ≤ l o g [ m / 2 ] [ ( N + 1 ) / 2 ] + 1 \log_m(N+1) \leq h \leq log_{[m/2]}[(N+1)/2]+1 logm(N+1)≤h≤log[m/2][(N+1)/2]+1
也就是说,存有N个关键码的m阶B-树的高度 h = Θ ( log m N ) h = \Theta (\log_m N) h=Θ(logmN)。
每次查找过程共需访问 O ( log m N ) O(\log_m N) O(logmN) 个节点,相应地需要做 O ( log m N ) O(\log_m N) O(logmN) 次外存读取操作。由此可知,对存有 N N N 个关键码的 m m m 阶B-树的每次查找操作,耗时不超过 O ( l o g m N ) O(log_m N) O(logmN)。
尽管没有渐进意义上的改进,但相对而言极其耗时的I/O操作的次数,却已大致缩减为原先的1/log2 m。
B-树:插入
关键码插入
template <typename T> boo BTree<T>::insert ( const T& e ){ //将关键码e插入B树中BTNodePosi(T) v = search ( e ); if ( v )return false; //确认目标节点不存在Rank r = _hot->key.search ( e ); //在节点_hot的有序关键码向量中查找合适的插入位置_hot->key.insert ( r + 1,e ); //将新关键码插至对应的位置_hot->child.insert ( r + 2,NULL ); //创建一个空子树指针_size++;//更新全树规模solveOverflow (_hot); //如有必要,需做分裂return true; //插入成功
}
为在B-树中插入一个新的关键码 e,首先调用search(e)在树中查找该关键码。若查找成功,则按照“禁止重复关键码”的约定不予插入,操作即告完成并返回false。
查找过程必然终止于某一外部节点v,且其父节点由变量_hot指示。当然,此时的_hot必然指向某一叶节点(可能同时也是根节点)。接下来,在该节点中再次查找目标关键码e。尽管这次查找注定失败,却可以确定e在其中的正确插入位置r。最后,只需将e插至这一位置。
至此,_hot所指的节点中增加了一个关键码。若该节点内关键码的总数依然合法(即不超过m - 1个),则插入操作随即完成。否则,称该节点发生了一次上溢(overflow),此时需要通过适当的处理,使该节点以及整树重新满足B-树的条件。
上溢与分裂
一般地,刚发生上溢的节点,应恰好含有 m m m 个关键码。若取 s = [ m / 2 ] s = [m/2] s=[m/2],则它们依次为: { k 0 , . . . , k s − 1 ; k s ; k s + 1 , . . . , k m − 1 } \{ k_0,...,k_{s-1};k_s;k_{s+1},...,k_{m-1} \} {k0,...,ks−1;ks;ks+1,...,km−1}。可见,以 k s k_s ks 为界,可将该节点分前、后两个子节点,且二者大致等长。于是,可令关键码 k s k_s ks上升一层,归入其父节点(若存在)中的适当位置,并分别以这两个子节点作为其左、右孩子。这一过程,称作节点的分裂。
实现
template<typename T> //关键码插入后若节点上溢,则做节点分裂处理
void BTree<T>::solveOverflow ( BTNodePosi(T) v ) {if (_order >= v->child.size() ) return; //递归基:当前节点并未上溢Rank s = _order / 2; //轴点(此时应有_order = key.size() = child.size() - 1)BTNodePosi(T) u = new BTNode<T>();//注意:新节点已有一个空孩子for ( Rank j= 0;j< _order - s - 1; j++ ) {//v右侧_order-s-1个孩子及关键码分裂为右侧节点uu->child.insert ( j,v->child.remove ( s +1));//逐个移动效率低u->key.insert ( j,v->key.remove ( s +1));//此策略可改进}u->child[_order - - 1] = V->child.remove ( s + );//移动v最靠右的孩子if ( u->child[e] ) //若u的孩子们非空,则for ( Rank j= ;j< _order - s; j++ ) //令它们的父节点统一u->child[j]->parent = u; //指向uBTNodePosi(T) p = v->parent; //v当前的父节点pif ( !p )[_root = p = new BTNode<T>(); p->child[0] = v; v->parent = p;} //若p空则创建之Rank r = 1 + p->key.search ( v->key[0] ); //p中指向u的指针的秩p->key.insert ( r,v->key.remove ( s ) ); //轴点关键码上升p->child.insert (r + 1,u );u->parent = p;//新节点u与父节点p互联solveOverflow ( p ); //上升一层,如有必要则继续分裂——至多递归O(logn)层
}
上溢持续传播至根的情况:原树根分裂之后,新创建的树根仅含单关键码。由此也可看出,就B-树节点分支数的下限要求而言,树根节点的确应该作为例外。
复杂度
若将B-树的阶次m视作为常数,则关键码的移动和复制操作所需的时间都可以忽略。至于solveOverflow()算法,其每一递归实例均只需常数时间,递归层数不超过B-树高度。由此可知,对于存有N个关键码的m阶B-树,每次插入操作都可在O(logm N)时间内完成。
B-树:删除
template <typename T> bool BTree<T>::remove ( const T& e ) { //从BTree树中删除关键码eBTNodePosi(T) v = search ( e ); if ( !v ) return false; //确认目标关键码存在Rank r = v->key.search ( e );//确定目标关键码在节点v中的秩(由上,肯定合法)if ( v->child[0] ) { //若v非叶子,则e的后继必属于某叶节点BTNodePosi(T) u = v->child[r+1]; //在右子树中一直向左,即可while ( u->child[0] ) u = u->child[0]; //找出e的后继v->key[r] = u->key[e]; v = u; r = 0; //并与之交换位置} //至此,v必然位于最底层,且其中第r个关键码就是待删除者v->key. remove ( r ); v->child.remove ( r + 1 ); _size--; //删除e,以及其下两个外部节点之一solveUnderflow ( v );// 如有必要,需做旋转或合并
return true;
为从 B-树中删除关键码 e,也首先需要调用 search(e) 查找 e 所属的节点。倘若查找失败,则说明关键码 e 尚不存在,删除操作即告完成:否则按照代码的出口约定,目标关键码所在的节点必由返回的位置v指示。此时,通过顺序查找,即可进一步确定e在节点v中的秩r。
不妨假定v是叶节点——否则,e的直接前驱(后继)在其左(右)子树中必然存在,而且可在O(height(v))时间内确定它们的位置,其中height(v)为节点v的高度。此处不妨选用直接后继。于是,e的直接后继关键码所属的节点u必为叶节点,且该关键码就是其中的最小者u[0]。既然如此,只要令e与u[0]互换位置,即可确保待删除的关键码e所属的节点v是叶节点。
接下来可直接将e(及其左侧的外部空节点)从v中删去。如此,节点v中所含的关键码以及(空)分支将分别减少一个。若该节点所含关键码的总数依然合法(即不少于[m/2] - 1),则删除操作随即完成。否则,称该节点发生了下溢,并需要通过适当的处置,使该节点以及整树重新满足 B-树的条件。
下溢与合并
在m阶B-树中,刚发生下溢的节点V必恰好包含[m/2] - 2个关键码和[m/2] - 1个分支。
1.V 的左兄弟 L 存在,且至少包含 [m/2] 个关键码
 将
将y从节点P转移至节点V中(作为最小关键码),再将x从L转移至P中(取代原关键码y)
2.V 的右兄弟 R 存在,且至少包含 [m/2]个
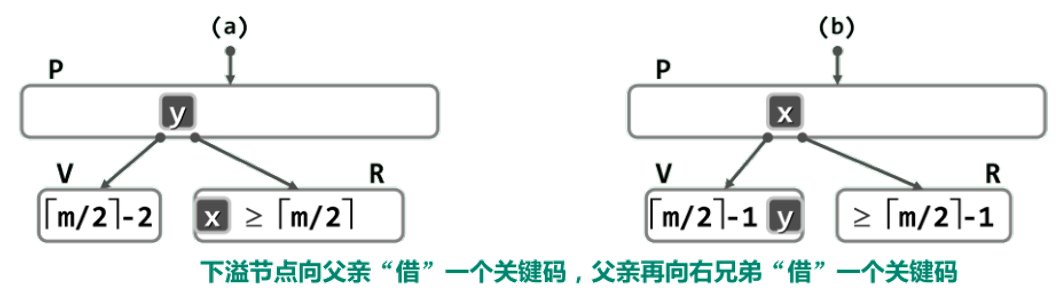
3.V 的左、右兄弟 L 和R 或者不存在,或者其包含的关键码均不足 [m/2] 个
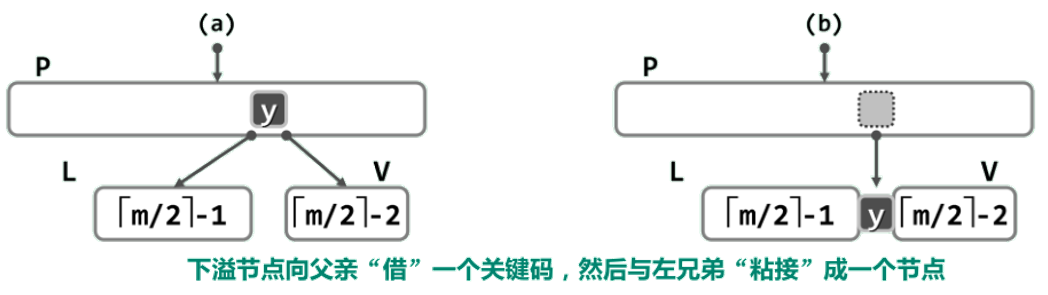
从父节点P中抽出介于L和V之间的关键码y,并通过该关键码将节点L和V“粘接”成一个节点——这一过程称作节点的合并。
在经如此合并而得新节点中,关键码总数应为:([m/2] - 1) + 1 + ([m/2] - 2) = 2*[m/2] - 2 <= m - 1
故原节点V的下溢缺陷得以修复,而且同时也不致于反过来引发上溢。
修复之后仍可能导致祖父节点以及更高层节点的下溢——这种现象称作下溢的传递。特别地,当下溢传递至根节点且其中不再含有任何关键码时,即可将其删除并代之以其唯一的孩子节点,全树高度也随之下降一层。
与上溢传递类似地,每经过一次下溢修复,新下溢节点的高度都必然上升一层。整个下溢修复的过程中至多需做O(log m N)次节点合并操作。
复杂度
与插入操作同理,在存有N个关键码的m阶 B-树中的每次关键码删除操作,都可以在O(logm N)时间内完成。另外同样地,因某一关键码的删除而导致 O ( l o g m N ) \mathcal O(log m N) O(logmN) 次合并操作的情况也极为罕见,单次删除操作过程中平均只需做常数次节点的合并。



















