动态博弈
0 引言
前面一篇文章介绍了博弈过程中的三个分类：静态博弈、动态博弈、重复博弈。今天具体讲讲动态博弈的处理方法。
博弈论——博弈过程
1 概念
首先还是介绍一下动态博弈的概念，即博弈中各博弈方的选择和行动不仅有先后次序，而且后选择、后行动的博弈方决策行为之前可以看到其他博弈方的决策行为，甚至包括双方的交替选择和行动。这种博弈无论哪种意义上都无法看作同时决策的静态博弈，我们称为“动态博弈”( dynamic games)、“多阶段博弈”(multistage games)或者“序列博弈(sequential games)”。根据例子可以更好地理解动态博弈，如下象棋就是典型的动态博弈，两位棋手在规则之内交替移动棋子，并且这个过程中，双方都可以看到对方的决策行为，又比如斯塔克尔伯格博弈中，领导者先做决策，追随者后做决策，也是一个动态过程。
动态博弈中，博弈方的选择有先后次序，通常将一个博弈方的一次选择称为一个“阶段”(stage)。动态博弈中也可能存在几个博弈方同时选择的情况，此时这些博弈方的同时选择构成一个阶段。一个动态博弈至少由两个阶段构成，所以动态博弈也被称为多阶段博弈。
2 动态博弈表示方法——扩展形
扩展形是一种简单明了的用于表示动态博弈的方法，该方法类似于树状图的结构，通过选择节点、从选择节点出发代表可能选择的线段，以及终端处得益数组三个要素来表示动态博弈。因为扩展形可以反映动态博弈中博弈方的选择次序和博弈阶段，是动态博弈的最佳表示方法。
下面举一个例子来进一步介绍扩展形：
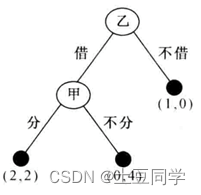
以开金矿博弈为例：甲开采一个价值四千万元的金矿时缺一千万资金，而乙正好有一千万闲置资金。甲想说服乙将资金借给自己开矿，许诺采到金子后双方对半分成。乙是否应该同意借钱？假设金矿价值经过权威部门探测确认且开采技术和销路都有保障，乙需要担心的只是甲采到金子后是否会履行诺言跟自己平分，还是会卷款潜逃。
我们用扩展形来表示这个博弈：最上面的圆圈表示乙的选择信息集，乙在此处有“借”和“不借”两种选择。乙选择“不借”则博弈结束，他能保住一千万元本钱，而甲得不到开矿利润，乙选择“借”则到达甲的选择信息集，轮到甲进行选择。甲可以选择“分”或“不分”。“分”则皆大欢喜，甲得两千万元开矿利润，乙的一千万元本钱增值成两千万元。若甲选择“不分”可以独吞四千万元，乙则血本无归。图中3个终端黑点处的数组表示两博弈方依次选择到达这些终端的“路径”实现的双方得益，其中第一个数字是乙的得益、第二个数字是甲的得益。
3 动态博弈特点
动态博弈主要有两个基本特点：
第一个特点在前面已经提到过，在动态博弈中，各个博弈方的选择和行为不仅有先后之分，还可能有多次，而且多次行为之间有内在联系，比如下象棋，每一位棋手在移动棋子的时候都会看到全局的棋子分布以及对方的行为选择。动态博弈中博弈方选择的不是博弈方在单个阶段的行为，而是在整个博弈中轮到选择的每个阶段，针对前面阶段的各种情况作相应选择的完整计划。动态博弈中博弈方的“策略"就是指这种计划。
第二个特点是非对称性。由于动态博弈中，博弈方的选择行为有先后次序且后行为者能观察到先行为博弈方的行为。先行为博弈方可能拥有先行的主动权，这是一种先行优势；后行为博弈方则可以相机作针对性的选择，而且有更多信息帮助选择行为，可能有后发制人的优势。动态博弈中究竟是先行有利还是后行有利并不确定，要根据具体博弈环境、利益关系决定。可以肯定的是,动态博弈的博弈方之间通常存在形势利益的某种不对称性。
