C-11 三角剖分算法
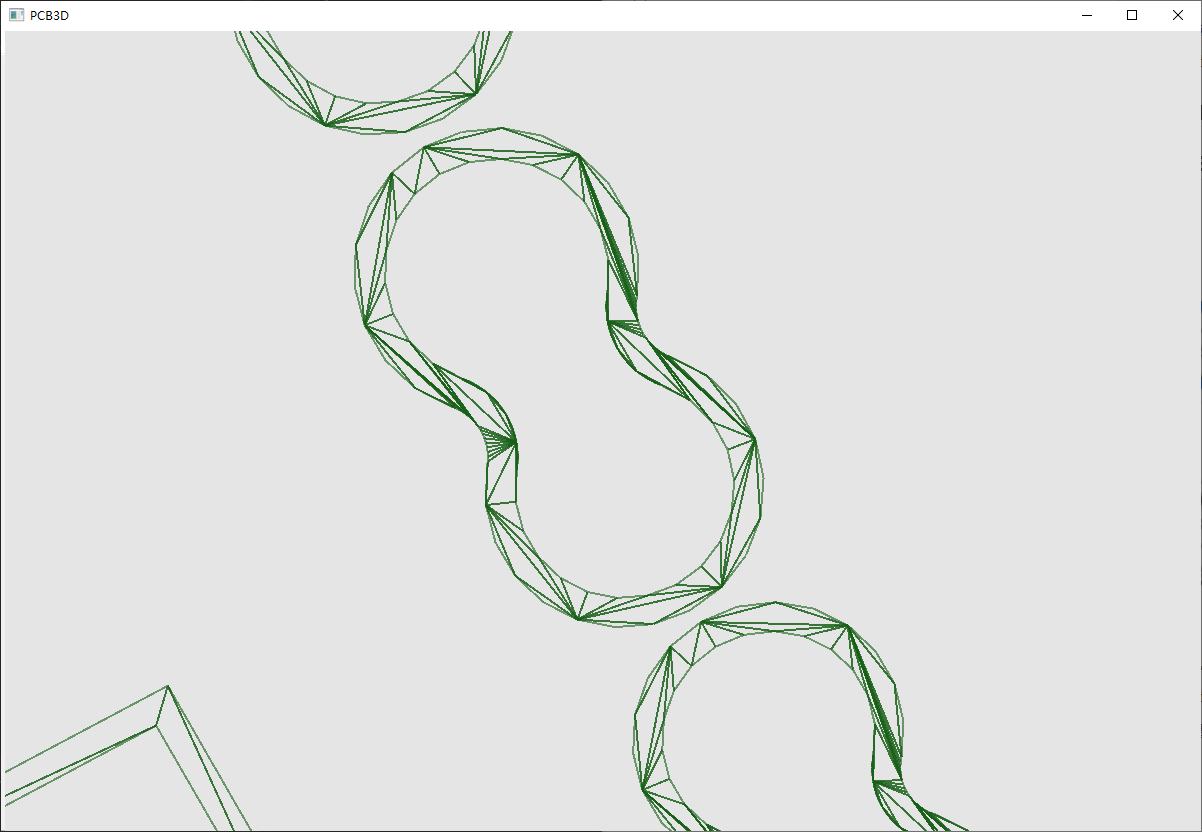
- 三角剖分就是将输入的多边形,分割成一系列互不重叠的三角形,其重要性就在这不多赘述。
- 这个是一个别人总结的链接:http://vterrain.org/Implementation/Libs/triangulate.html

图片链接:http://www-cgrl.cs.mcgill.ca/~godfried/teaching/cg-projects/97/Thierry/thierry507webprj/complexity.htm
耳切割算法 (eat-cut) O ( n 3 ) O(n^3) O(n3)
- 可以生成带孔多边形的算法
- GitHub地址: https://github.com/mapbox/earcut.hpp
- 这是生成凹多边形的算法,简单来说,凹下去的那一个顶点就是耳朵,先生成多边形的凸包,然后找到该多边形上凹下去的顶点,把那部分给“切”掉,这就是而且个算法
#include <earcut.hpp>// The number type to use for tessellation
using Coord = double;// The index type. Defaults to uint32_t, but you can also pass uint16_t if you know that your
// data won't have more than 65536 vertices.
using N = uint32_t;// 创建多边形
using Point = std::array<Coord, 2>;
std::vector<std::vector<Point>> polygon;//放入轮廓线
polygon.push_back({{100, 0}, {100, 100}, {0, 100}, {0, 0}});
//放入洞,除了第一条线是轮廓线之外,从第二条线开始就是洞线了
polygon.push_back({{75, 25}, {75, 75}, {25, 75}, {25, 25}});//返回索引值
std::vector<N> indices = mapbox::earcut<N>(polygon);
//读取索引值就是离散化完成的三角形了
Delaunay三角剖分算法 O ( n log n ) O(n\log n) O(nlogn)
- 普通的Delaunay三角剖分算法不能对带孔多边形进行三角剖分
约束Delaunay三角剖分算法 (CDT) O ( n log n + m log n ) O(n\log n+m\log n) O(nlogn+mlogn)
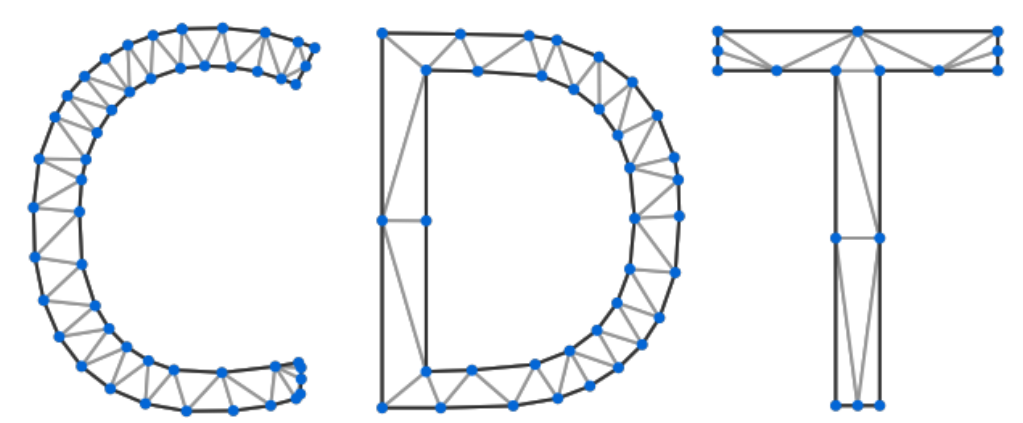
- CGAL几何库采用的就是这种三角剖分算法,因此无论是时间上还是稳定性上这种算法都是值得信赖的
- 时间复杂度中的m是指轮廓边和孔洞边的数量
- GitHub地址: https://github.com/artem-ogre/CDT
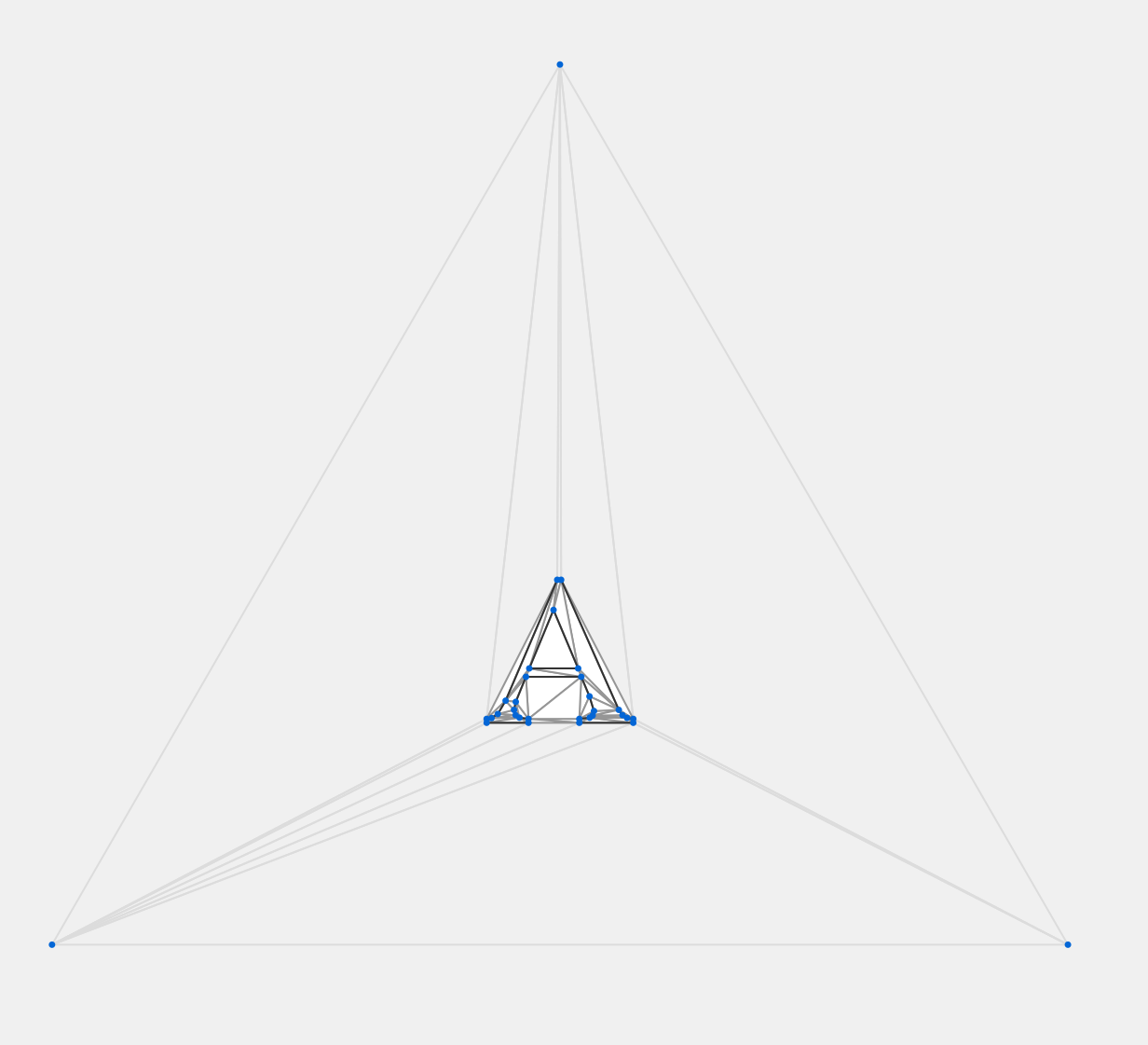
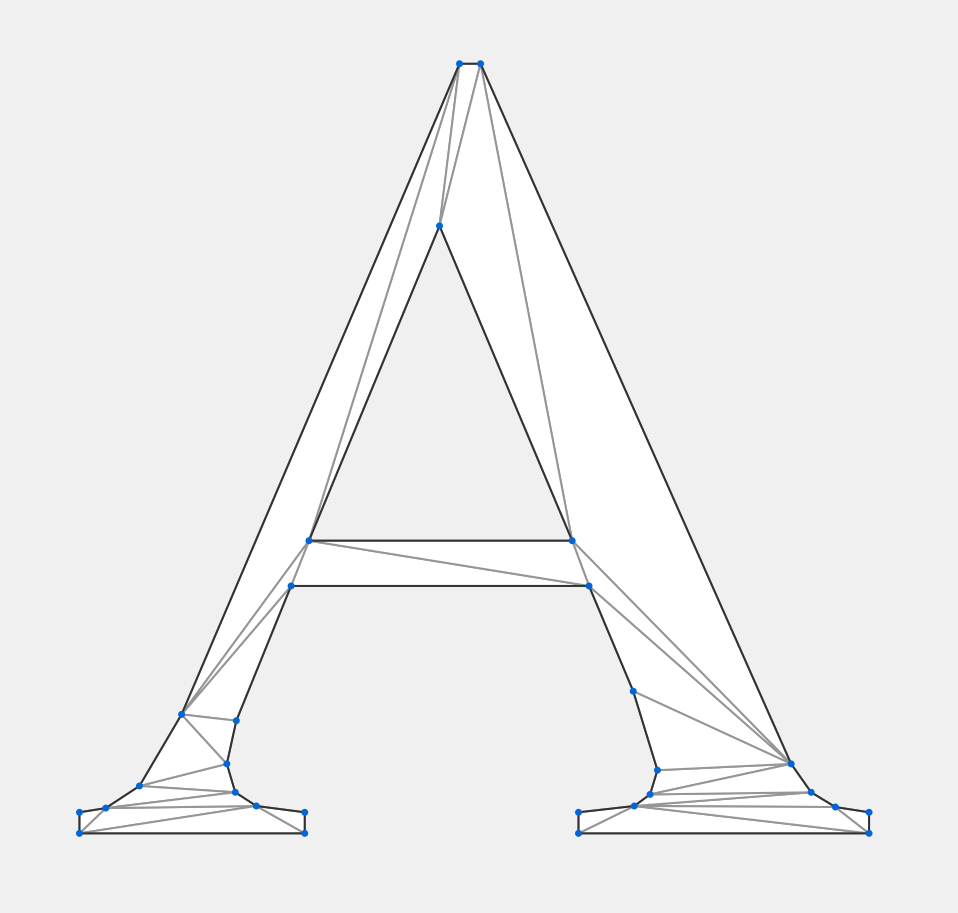
- 算法步骤
- 和Delaunay一样 先生成super triangle
- 然后剔除super triangle带来的边
- 剔除外轮廓边之外的边
- 剔除孔洞之中的边
单调多边形三角化
- 这个我也没大看懂,也没有自己代码实现过,所以不敢妄言
- 简单的说一说就是把一个多边形分成若干个单调多边形(Monotone Polygon)。然后将单调多边形进行三角剖分
- 单调多边形是指一个有两条链子组成的多边形,然后两条链子上的顶点的纵坐标是递增的或者横坐标是递增的。比如下面是一个y单调多边形,就是纵坐标递增。坐标相等也算递增,比如长方形也是单调多边形。
- 这个思想就很有意思,就如同红黑树一样,介于平衡二叉树和普通二叉树之间。单调多边形就介于凸多边形和凹多边形之间。凸多边形必然是一个单调多边形,而凹多边形就不一定了。
- 把一个多边形分成单调多边形的过程(line sweep)的时间复杂度是O(nlogn),而对一个单调多边形进行三角划分的时间复杂度是O(n);
- https://www.cnblogs.com/dogstar/archive/2011/04/07/2008726.html 这个大佬的博客有多边形单调划分相关步骤的说明。也有单调多边形三角化的说明,可以看看
- 在计算几何算法与应用这本书里面,也有算法的详细说明
- 《计算几何算法与应用(第三版)》 链接:https://pan.baidu.com/s/1exLpWuD5cBcZGasWH8Y3_w 提取码:6666



其他的剖分算法
- https://www.flipcode.com/archives/Efficient_Polygon_Triangulation.shtml
- http://www.cs.unc.edu/~dm/CODE/GEM/chapter.html
参考资料
- 一个多边形三角剖分汇总网站 http://vterrain.org/Implementation/Libs/triangulate.html
- 《J. O’Rourke, Computational in C, 2nd Edition》链接:https://pan.baidu.com/s/1E4tYKPJ2miU9OXRpw0tWng 提取码:6666


、重载的理解)



)






![洛谷 P3008 [USACO11JAN] Roads and Planes G](http://pic.xiahunao.cn/洛谷 P3008 [USACO11JAN] Roads and Planes G)





