---

1.背景

2024年，A Taheri受到部分强化效应(PRE)理论启发，提出了局部强化优化算法（Partial Reinforcement Optimizer, PRO）。

2.算法原理

2.1算法思想

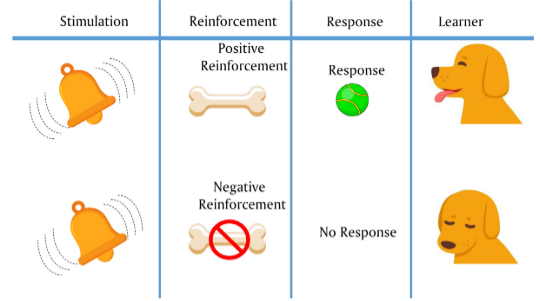
PRO来自进化学习和训练的心理学理论，称为部分强化效应(PRE)理论。根据PRE理论，学习者在学习和训练过程中间歇性地强化学习或加强特定的行为。通过选择适当的强化行为和实施强化过程的时间，强化模式显著影响学习者在强化计划中的反应率和强度。

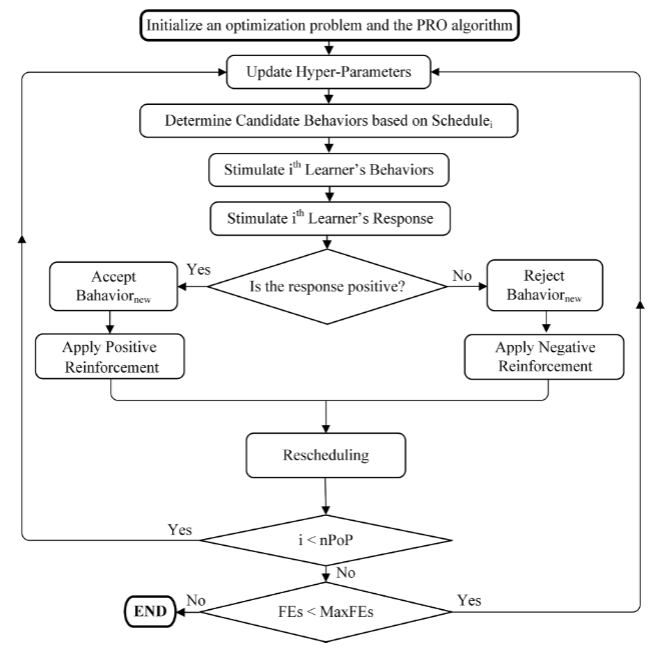
2.2算法过程

调度

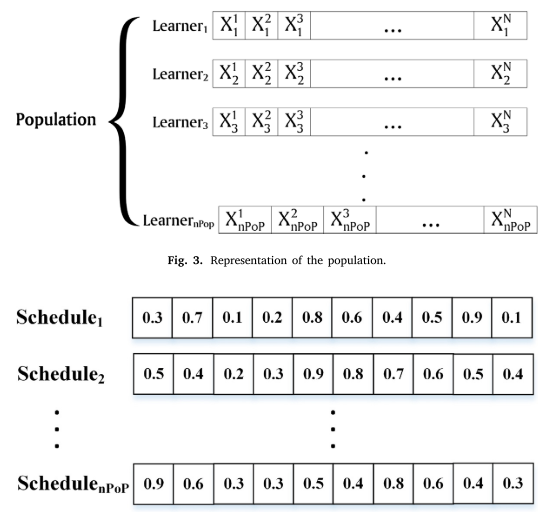
调度是指如何以及何时需要加强行为，在不同的时间间隔内为数据结构建模。每个学习者都有一个特定的时间表，由于每个标量代表了特定学习者行为的分数优先级，分数优先级越高，下一次迭代中被选择的机会就越大。将调度中的优先级按降序排序：
τ ← F E s M a x F E s S R ← e − ( 1 − τ ) μ ⊆ { 1 , 2 , 3 , … , N } ∣ ∀ j ∈ μ , S c h e d u l e j ≥ S c h e d u l e ∗ , λ , λ ← { ∥ μ ∥ ∣ ∥ μ ∥ = [ U ( 1 , N × S R ) ] } (1) \begin{aligned} &\tau\leftarrow\frac{FEs}{MaxFEs} \\ &SR\leftarrow e^{-(1-\tau)} \\ &\mu\subseteq\{1,2,3,\ldots,N\}\quad| \forall j\in\mu, Schedule^{j} \geq Schedule^{*,\lambda}, \\ &\lambda\leftarrow\{ \|\mu\| | \|\mu\|=[U(1, N\times SR)] \} \end{aligned}\tag{1} ​τ←MaxFEsFEs​SR←e−(1−τ)μ⊆{1,2,3,…,N}∣∀j∈μ,Schedulej≥Schedule∗,λ,λ←{∥μ∥∣∥μ∥=[U(1,N×SR)]}​(1)
其中，$\tau$为时间因子，FEs为函数评价的次数，MaxFEs为函数评价的最大次数。其中，SR是选择率，gr是基于调度选择的行为子集，gr是选择子集的大小，是行为(决策变量)的总数。

刺激

任何试图刺激学习者的行为以引起反应的尝试都是通过应用操作来改变所提出的解决方案的决策变量来建模。使用以下操作来生成新的解：
$$\begin{array}{rl}& S{F}_i\leftarrow \tau +U(0,\bar{\beta }),\mathrm{where}\bar{\beta }\leftarrow \sum _{j\in \mu }\left(\frac{Schedul{e}_{i,j}}{Max\left(Schedul{e}_i\right)}\right)\\ & S_i^{\mu }\leftarrow \{\begin{array}{ll}(X_{best}^{\mu }-X_i^{\mu })& \text{If rand < 0.5}\\ (X_i^{\mu }-X_j^{\mu })& \text{Otherwise.}\end{array}\\ & X_{i,new}^{\mu }\leftarrow X_i^{\mu }+S{F}_i\times S_i^{\mu }\end{array}\text{\hspace{1em}(2)}$$

强化

应用正强化来增加特定行为的分数，学习者的目标函数作为刺激阶段改进后的响应:
$$Schedul{e}_i^{\mu }\leftarrow Schedul{e}_i^{\mu }+(Schedul{e}_i^{\mu }\times RR)\text{\hspace{1em}(3)}$$
其中，RR为强化率。当没有反应时，就会施加负强化。在这种情况下，学习者的目标函数在刺激阶段后减小，导致特定行为得分下降：
$$Schedul{e}_i^{\mu }\leftarrow Schedul{e}_i^{\mu }-(Schedul{e}_i^{\mu }\times RR)\text{\hspace{1em}(4)}$$

重新调度

在训练过程中为学习者应用一个新的时间表，当学习者的所有行为都持续受到负强化时。在这种情况下，PRO利用计划的标准偏差(Std)作为度量来确定何时需要重新安排学习者的计划:
$${\text{Schedule}}_{\mathrm{i}}\leftarrow \{\begin{array}{l}U(0,1){\text{if Std(Schedule}}_{\mathrm{i}})=0\\ Do\text{nothing}\text{otherwise}\end{array}\text{\hspace{1em}(5)}$$
$${\mathrm{X}}_{\mathrm{i}}\leftarrow \{\begin{array}{cc}U(L_B,U_B)& \mathrm{if}\mathrm{Std}(\mathrm{Schedul}{\mathrm{e}}_{\mathrm{i}})=0\\ Do\text{nothing}& \mathrm{otherwise}\end{array}\text{\hspace{1em}(6)}$$

流程图

伪代码

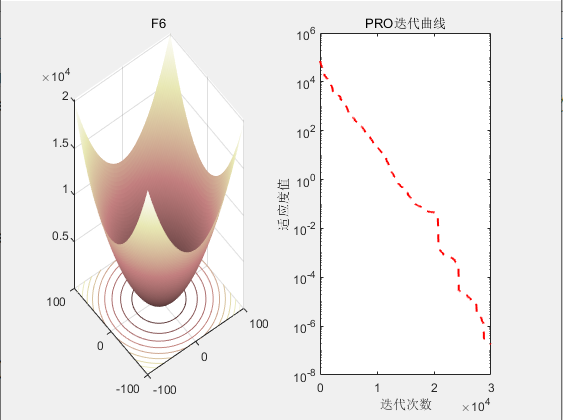
3.结果展示

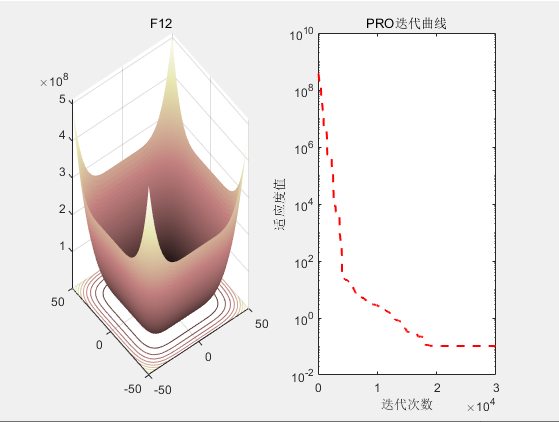
4.参考文献

[1] Taheri A, RahimiZadeh K, Beheshti A, et al. Partial reinforcement optimizer: An evolutionary optimization algorithm[J]. Expert Systems with Applications, 2024, 238: 122070.

5.代码获取