一、【实验目的】
(1)进一步理解贪心法的设计思想
(2)掌握哈夫曼算法的具体应用
(3)比较不同的文件归并策略,探讨最优算法。
二、【实验内容】
设S={f1,…,fn}是一组不同的长度的有序文件构成的集合,其中fi表示第i个文件的记录个数,现使用二分归并法将这些文件归并成一个有序文件,归并过程可以看成是一棵二叉树.参考教材P102例4.7,请采用两种方法进行二分归并,其中一种为哈夫曼算法。
提示:其中n个文件可用n个数组模拟,文件的内容为数组中已排好序的整数;可以用教材例4.7中定义的S集合中6个文件的长度作为数组长度进行测试。注意,要编写两个数组进行顺序归并的程序。
三、实验源代码
四、实验结果
五、实验分析与总结
实验分析:
要求完成以下两种归并
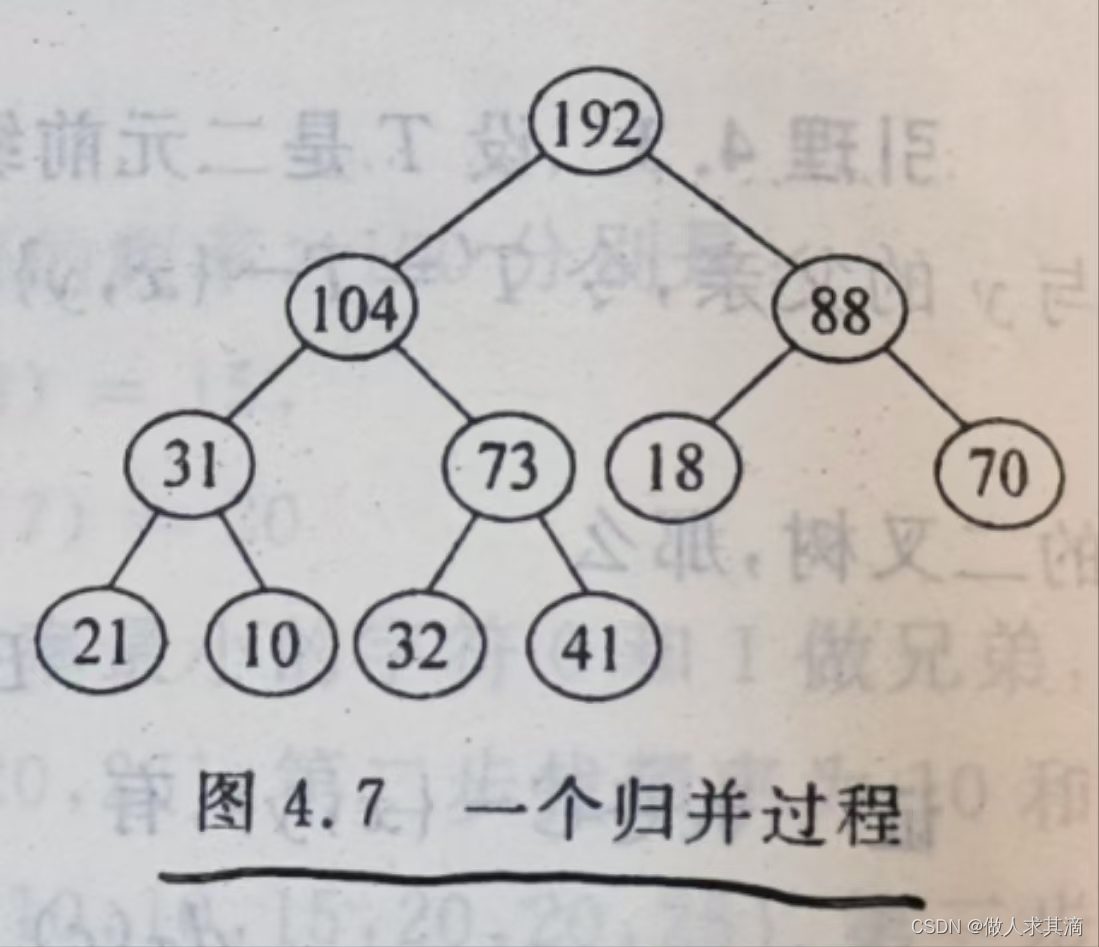

按照哈夫曼算法的思路,先取最小的两个点进行归并,得到一个父结点。再放回去再选择两个小的。
⚠️错误写法
- 这里用的优先队列实现了插入一个元素后排序且可以有队列的特性。
- j用于叶子结点的创建,i用于父结点的创建。
- returnElement函数取最小的两个元素,再加起来放回去
#include <bits/stdc++.h>
using namespace std;int n = 6;
vector<int> s = {21, 10, 32, 41, 18, 70};
vector<int> a = s;
vector<int> temp(10);
priority_queue<int, vector<int>, greater<int>> pq; //升序队列模板struct treeNode{int weight;int parent;int leftchild, rightchild;
}tree[20];void returnElement(int& element1, int& element2)
{if(!pq.empty()){element1 = pq.top();pq.pop();element2 = pq.top();pq.pop();int sum = element1 + element2;pq.push(sum);}
}void CreateHuffmanTree(){ //二分归并法最优//输入for(auto e : s)pq.push(e);int j=1, element1, element2;//初始化-1for(int i=1; i<=2*n-1; i++){tree[i].parent = -1, tree[i].leftchild = -1; tree[i].rightchild = -1;}for(int i=n; i<=2*n-1; i++){//左右孩子结点returnElement(element1, element2);tree[j].weight = element1;j++;tree[j].weight = element2;j++;//父节点tree[i].weight = element1 + element2;tree[i].leftchild = j-2;tree[i].rightchild = j-1;}}
//由于中文乱码,所以输出英文
void printTree()
{for (int i = 1; i <=2*n-1; i++){cout << setw(7) << "i:" << i ;cout << setw(7) << "node:" << tree[i].weight << "\t";cout << setw(7) << "parent:" << tree[tree[i].parent].weight << "\t";cout << setw(7) << "leftchild:" << tree[tree[i].leftchild].weight << "\t";cout << setw(7) << "rightchild:" << tree[tree[i].rightchild].weight << endl;}
}int main()
{CreateHuffmanTree();printTree();return 0;
}运行结果:
- 叶子结点和父结点交叉存放
- -1的值未打印出来
- 有一些数据被覆盖掉了
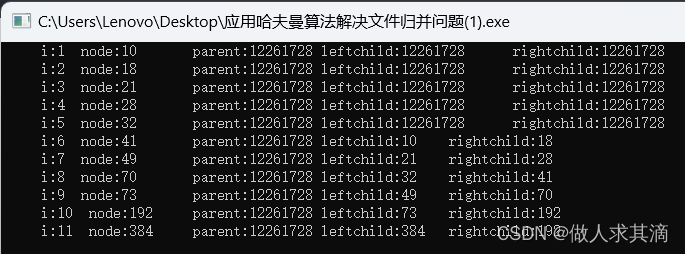

对比书上的图,缺项多项
正确写法:
【【数据结构】构造哈夫曼树手写代码】![]() https://www.bilibili.com/video/BV1EV4y1V7Vx/?share_source=copy_web&vd_source=7ffbd7feaeedb3d59fb21e59435a53d8 改进:
https://www.bilibili.com/video/BV1EV4y1V7Vx/?share_source=copy_web&vd_source=7ffbd7feaeedb3d59fb21e59435a53d8 改进:
returnElement函数弃用,改成每次在tree中寻找最小元素、和次小元素的下标。
先把叶子结点存入,以免出现交叉存放和覆盖数据
先把叶子结点存入后,直接更新父结点的值就可以了,叶子结点的parent指向父结点的下标
#include <bits/stdc++.h>
using namespace std;int n = 6;
vector<int> s = {21, 10, 32, 41, 18, 70};
vector<int> a = s;
vector<int> temp(10);
//priority_queue<int, vector<int>, greater<int>> pq; //升序队列模板struct treeNode{int weight;int parent;int leftchild, rightchild;
}tree[20];void selectMinElementIndex(int n, int& index1, int& index2)
{int min = 9e8; //打擂台,用于确定最小的那个//寻找最小的权值下标for(int i=1; i<= n; i++){if(tree[i].parent == -1 && tree[i].weight < min){min = tree[i].weight;index1 = i;}}min = 9e8;//寻找次小的权值下标for(int i=1; i<= n; i++){if(tree[i].parent == -1 && tree[i].weight < min && i != index1){min = tree[i].weight;index2 = i;}}
}void CreateHuffmanTree(){ //二分归并法最优sort(s.begin(), s.end()); int index1, index2;//初始化-1for(int i=1; i<=2*n-1; i++){tree[i].parent = -1, tree[i].leftchild = -1; tree[i].rightchild = -1;}//放入叶子结点for(int i=1; i<=n; i++){tree[i].weight = s[i-1];}for(int i=n+1; i<=2*n-1; i++){//传入了i-1,保证在新建立的父节点和叶子结点中寻找两个最小selectMinElementIndex(i-1, index1, index2);// 左右孩子结点指向父结点tree[index1].parent = i;tree[index2].parent = i;//父结点更新值tree[i].weight = tree[index1].weight + tree[index2].weight;tree[i].leftchild = index1;tree[i].rightchild = index2;}
}
//由于中文乱码,所以输出英文
void printTree()
{for (int i = 1; i <= 2*n-1; i++){cout << setw(7) << "i:" << i << " ";cout << setw(7) << "node:" << tree[i].weight << "\t";cout << setw(7) << "parent:" << (tree[i].parent != -1 ? tree[tree[i].parent].weight : -1) << "\t";cout << setw(7) << "leftchild:" << (tree[i].leftchild != -1 ? tree[tree[i].leftchild].weight : -1) << "\t";cout << setw(7) << "rightchild:" << (tree[i].rightchild != -1 ? tree[tree[i].rightchild].weight : -1) << endl;}
}void CreateATree(){ //另一种二分归并法int j=1;//初始化-1for(int i=1; i<=2*n-1; i++){tree[i].parent = -1, tree[i].leftchild = -1; tree[i].rightchild = -1;}//放入叶子结点for(int i=1; i<=n; i++){tree[i].weight = s[i-1];}for(int i=n+1; i<=2*n-1; i++){// 左右孩子结点指向父结点,j直接选两个平推过去tree[j].parent = i;tree[j+1].parent = i;//父结点更新值tree[i].weight = tree[j].weight + tree[j+1].weight;tree[i].leftchild = j;tree[i].rightchild = j+1;j += 2;}
}int main()
{cout << "The another method:" << endl;CreateATree();printTree();cout << "The best method:" << endl;CreateHuffmanTree();printTree();return 0;
}【运行结果】
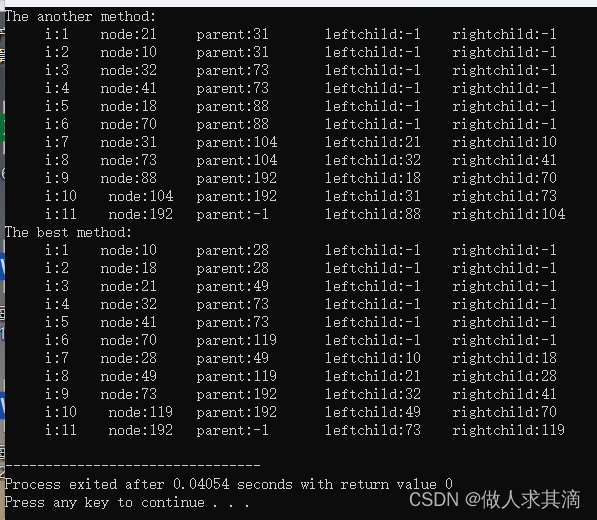









)



)





