文章目录
- 0. 基本知识
- 1.三相的电压之和为0
- 2.正弦交流相量的相量表示法(相量只是表示正弦量,而不等于正弦量 ;只有正弦量才能用相量表示)
- 引入相量表示法目的:
- 一种正弦量的产生方式:
- 正弦量的相量表示,使用欧拉公式表示复数
- 3.用复数表示正弦量,并进行计算
- 4.电力电子中的坐标变换详解(clark变换、park变换, 3/2变换、旋转变换)
- 1.为何需要进行坐标变换?
- 2.clark变换(ABC轴到αβ0轴的坐标变换)
- 1.电压转换
- 2.(推荐使用最终形态的变换公式)电流clark转换和逆变换,等幅值变换需乘以2/3
- 3.park变换
- 5.SVM空间矢量调制
- 术语
- 相电压和线电压
- 共模电压
- 直流母线电压Vdc
- 理想的三次谐波
- 直流母线电压利用率和调制比
- 马鞍波
- 准比例谐振(QPR)
- SVM的优点
- 参考文档
- 其它问题
- 1.为何不用PID控制正弦输入?
- 参考文档
0. 基本知识
1.三相的电压之和为0
若以电压幅值是R(为了方便理解三个向量的计算值),则三个都是R,那么它们的和就是R*[cos(φ)+cos(φ+2Π/3)+cos(φ+4Π/3)],根据周期性,化简得三个和R*[cos(φ)+cos(φ+2Π/3)+cos(φ-2Π/3)]=R*[cos(φ)+2cos(φ)cos(2Π/3)]=0,
2.正弦交流相量的相量表示法(相量只是表示正弦量,而不等于正弦量 ;只有正弦量才能用相量表示)
引入相量表示法目的:
将正弦相量转为复数形式的向量后,方便计算;

一种正弦量的产生方式:
一个绕原点以角速度w逆时针匀速旋转的有向线段,每一瞬时在纵轴上的投影即表示为相应时刻正弦量的瞬时值;

正弦量的相量表示,使用欧拉公式表示复数

- 使用欧拉公式可以将正弦量用复数表示,如下:

3.用复数表示正弦量,并进行计算
- 复数的虚部可以表达正弦量
4.电力电子中的坐标变换详解(clark变换、park变换, 3/2变换、旋转变换)


1.为何需要进行坐标变换?
- 1.简化电机数学模型,磁的耦合越少越简单

- 2.clark变换(ABC轴到αβ0轴的坐标变换):三相电机模型到两相平衡交流电机模型的简化


- 3.park变换(αβ0轴到dq0轴的坐标变换): 两相平衡交流电机模型 ==》两 相直流电机模型


2.clark变换(ABC轴到αβ0轴的坐标变换)
1.电压转换
- 三相交流电电压和坐标系(ua,ub,uc合成幅值不变且逆时针旋转的矢量)
 |
|

2.将正弦量ua,ub,uc拆分为在αβ坐标系的矢量表示为V:
把A轴对应的θ角定为0度,则A,B,C三相坐标系上的正弦矢量可分别表示ua,ub, uc,如下 :
使用欧拉公式,将ua,ub, uc表示为在αβ坐标系的矢量形式(θ角定为0度),这样就将三个正弦量拆分为αβ坐标系的矢量,可以进行加减运算:
正弦量Ua,Ub,Uc在αβ坐标系的矢量和为V,其表达式如下:
- 等幅值变换 * (2/3):公式推导及仿真验证:
|三相交流电电压代人
|
|
|
|
2.(推荐使用最终形态的变换公式)电流clark转换和逆变换,等幅值变换需乘以2/3
 恒流*2/3
恒流*2/3

为保持等幅值需乘以2/3,原理通电压转换式7:




- 最终的变换公式(带0轴I0,三相4线时如果三相幅值不相等时即三相不平衡),反变换则直接线性代数的知识求逆即可:
下式说明,从静止三相ABC变换到静止αβ绕组中通以互差90度的与三相同频率的两相平衡正弦交流电流,即可获得与三相静止
绕组等效的磁动势。
当Ia,Ib,Ic不对称时,总存在三相对称电流, I’a, I’b, I’c使得:
I’a = Ia - Io
I’b =. Ib - Io
I’c. = Ic - Io
由三相电的性质得 I’a +I’b + I’a = 0 ⇒ Io = 1/3 * (Ia +Ib + Ia) = 2/3 * 1/2(Ia +Ib + Ia). //恒流变换提出2/3系数
clark等幅值变换:

逆clark变换:

3.park变换
下式说明,在D Q轴上通以两个直流电流,其大小分别为三相绕组中的有功电流和无功电流;
这样也可获得与三相绕组等效的磁动势。
通过坐标分解,就是将αβ0坐标系上合成的矢量,分别投影到旋转坐标系的d轴和q轴上.

-
为简化处理,现在进行归一化处理,给定电压幅值为1的正弦量,分别用sin cos的形式表示:
将Um设为1,时的电压余弦表示或正弦表示:
将三相cos形式电压表达式代入A轴与d轴起始位置重合的旋转坐标变换公式 :
余弦表示电压:
可以得到:Vd==1, Vq == 0; 此时d是主控轴, 给定cos信号时使得d轴分量为1,所以是基于cos型的坐标系;
当电压幅值为Um时,Vd=Um, Vq=0; -
同理三相电流的计算方式相同:
>
5.SVM空间矢量调制
术语
相电压和线电压
-
1.相电压表达式:

-
2.线电压 Vac = Va - Vc

共模电压
加在电压表两测量端和规定公共端之间的那部分输入电压的三分之一,即(Va+Vb+Vc)/3。
直流母线电压Vdc
理想的三次谐波
马鞍波本质是正弦波叠加了基波三倍频率三角波得到的波形。
采用三次谐波注入技术后,级联H桥大功率变流器输出电压有效值更高、谐波含量更低,从而大大改善了系统的性能。


1.三次谐波注入方法研究
直流母线电压利用率和调制比

直流母线电压给定为VD时, 逆变器输出相电压Uan最大为2VD/3(即电压幅值);
即**(100组合)矢量作用下三相电压(VAn=2VD/3, VBn=-VD/3, VCn=-VD/3),三个矢量合成结果为VD,方向沿A轴正向,同理可求出其他5个非零基本矢量的幅值和方向。
由于逆变器和调制方式的能力限制,不能输出幅值为Udc的合成矢量圆,只能输出矢量六边形。
所以,减小参考合成矢量幅值,直到为VD*sqrt(3)/2,此时,输出幅值为VDsqrt(3)/2的合成矢量圆(为六边形内切圆),
此时相电压幅值为VDsqrt(3)/22/3=VDsqrt(3)/3**(根据基本的空间、时间依次差120°三相平衡电压合成矢量结果,相电压与合成矢量幅值的3/2倍关系),线电压的幅值为(VD*sqrt(3)/3)*sqrt(3)=VD,(该状态下的线电压幅值与直流电压的比值为直流电压利用率=1)。
现在有一点小问题是,相电压幅值为VDsqrt(3)/3,合成矢量幅值为VDsqrt(3)/2,我们关注的这两个变量幅值不相等,看着有些不方便,还要转化一下,我们让合成矢量的幅值缩小1.5倍,所有情况下的合成矢量幅值与相电压幅值就一样了啊!(过程是通过克拉克变换完成,所以将基本非零矢量的幅值缩小为我们常见的2/3 * VD了)
所以:
1.合成矢量幅值变为VRmax = (2/3) VDsqrt(3)/2 = VD*sqrt(3)/3 = 0.577VD, 因此SVPWM调制的相电压峰值是直流母线电压的0.577倍;
2.线电压是sqrt(3) VDsqrt(3)/3 =VD(等于直流母线电压)
3.SVPWM/SPWM= 0.57/0.5 = 1.1547;所以SVM产生的马鞍波使得直流母线电压的利用率有了很大提高
马鞍波
SVPWM,就产生了马鞍波,马鞍波也会产生正弦波的电流,。
马鞍波将波拉宽了,就代表高电压的持续时间变长了,提高了母线电压利用率(就是你的电池或者电源释放的电压),电机的动态响应更好。
当调制比都是1的时候:
SPWM相电压的峰值是母线电压的0.5倍,而SVPWM(就是FOC用的啦),是0.577倍,就是√3/3;
SPWM线电压的峰值是母线电压的0.866倍,而SVPWM,是1倍;
SVPWM/SPWM=1.1547;所以SVM产生的马鞍波使得直流母线电压的利用率有了很大提高。


准比例谐振(QPR)
SVM的优点
空间电压矢量PWM与传统的正弦PWM不同,它是从三相输出电压的整体效果出发,着眼于如何使电机获得理想圆形磁链轨迹。SVPWM技术与SPWM相比较,绕组电流波形的谐波成分小,使得电机转矩脉动降低,旋转磁场更逼近圆形,而且使直流母线电压的利用率有了很大提高,且更易于数字化实现。

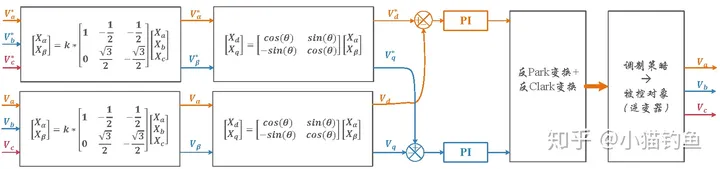
将参考电压Vd(将参考三相电压Va,Vc,Vc经clark和park变换计算得到)和反馈的Vd之间的偏差做PI计算控制:
参考文档
1.用于电机控制的空间矢量调制 (SVM)
其它问题
1.为何不用PID控制正弦输入?
用PI控制器对正弦输入进行跟踪时,会存在稳态误差。
参考文档
1.电工学 哈尔滨工业大学 姜三勇等主讲
2.搞懂电力电子中的坐标变换
3.电力电子中的坐标变换详解(clark变换、park变换, 3/2变换)
3.Clarke - Park transformation
5.手撕系列(2):Clark变换与Park变换