目录
简述
评估回归
模拟退火训练
政安晨的个人主页:政安晨
欢迎 👍点赞✍评论⭐收藏
收录专栏: 政安晨的机器学习笔记
希望政安晨的博客能够对您有所裨益,如有不足之处,欢迎在评论区提出指正!
简述
深度学习神经网络的评估回归是一种用于评估网络性能的方法。
在回归问题中,神经网络被用于将输入数据映射到连续的输出。
评估回归的目标是通过计算网络的输出和真实值之间的差异来评估网络的准确性。常见的评估指标包括均方误差(MSE)和平均绝对误差(MAE)。这些指标可以用来度量预测值与真实值之间的接近程度,从而评估网络的性能。
模拟退火是一种用于训练深度学习神经网络的优化算法。
该算法通过模拟物质在冷却过程中的结构优化过程来寻找全局最优解。在模拟退火算法中,网络的权重和偏差被视为系统的状态变量,优化过程被视为一个寻找最低能量状态的问题。通过迭代地调整网络的权重和偏差,并根据能量函数(即损失函数)计算网络的性能,模拟退火算法可以逐渐优化网络的参数,从而提高网络的性能。
在模拟退火训练中,初始温度被设置为一个比较高的值,然后通过不断迭代降低温度,从而控制系统的状态在搜索空间中移动的程度。每次迭代中,根据能量差和当前温度计算一个概率,用于决定是否接受新的状态。这样,模拟退火算法可以在搜索空间中探索较广的范围,并有可能避免陷入局部最优解。
通过评估回归和模拟退火训练,可以有效地评估和优化深度学习神经网络的性能,从而提高网络的准确性和泛化能力。
评估回归
均方差(MSE)计算是评估回归机器学习的最常用方法。大多数神经网络、支持向量机和其他模型的示例都采用了MSE,如下公式所示:
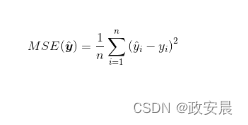
在上面公式中,y[i]是理想输出,y[i]^是实际输出。均方差的本质是各个差的平方的均值。因为对单个差求平方,所以差的正负性不影响MSE的值。
你可以用MSE评估分类问题。
为了用MSE评估分类输出,每个分类的概率都被简单地看成数字输出。对于正确的类,预期的输出就是1.0,对于其他类,预期的输出则为0。如果第一类是正确的,而其他三类是错误的,则预期结果向量将如下:
[1.0, 0, 0, 0]
这样,你几乎可以将任何回归目标函数用于分类。各种函数,如均方根(Root Mean Square,RMS)和误差平方和(Sum of Squares Error,SSE),都可以用于评估回归。
模拟退火训练
要训练神经网络,必须定义它的任务。目标函数(也称为计分或损失函数)可以生成这些任务。本质上,目标函数会评估神经网络并返回一个数值,表明该神经网络的有用程度。训练会在每次迭代中修改神经网络的权重,从而提高目标函数返回的值。
模拟退火是一种有效的优化技术,已在本系列的前文中提及,我们将回顾模拟退火,展示任意向量优化函数如何改善前馈神经网络的权重。
回顾一下,模拟退火的工作原理是首先将神经网络的权向量赋为随机值,然后将这个向量看成一个位置,程序会评估从该位置开始的所有可能移动。要了解神经网络权重向量如何转换为位置,请考虑只有3个权重的神经网络。在现实世界中,我们用x、y和z坐标来考虑位置。我们可以将任意位置写成有3个分量的向量。如果我们希望只在其中1个维度上移动,那么向量总共可以在6个方向上移动。我们可以选择在x、y或z维度上向前或向后移动。
通过在所有可用的维度上向前或向后移动,模拟退火实现其功能。如果该算法采取了最佳移动,那么将形成简单的爬山算法。爬山只会提高得分,因此,它也被称为贪心算法。为了达到最佳位置,算法有时需要移到较低的位置。因此,模拟退火很多时候有进两步、退一步的表现。
换言之,模拟退火有时会允许移动到具有较差得分的权重配置。接受这种移动的概率开始很高,而后逐渐降低。这种概率称为当前温度,它模拟了实际的冶金退火过程。
下图展示了模拟退火的整个过程。
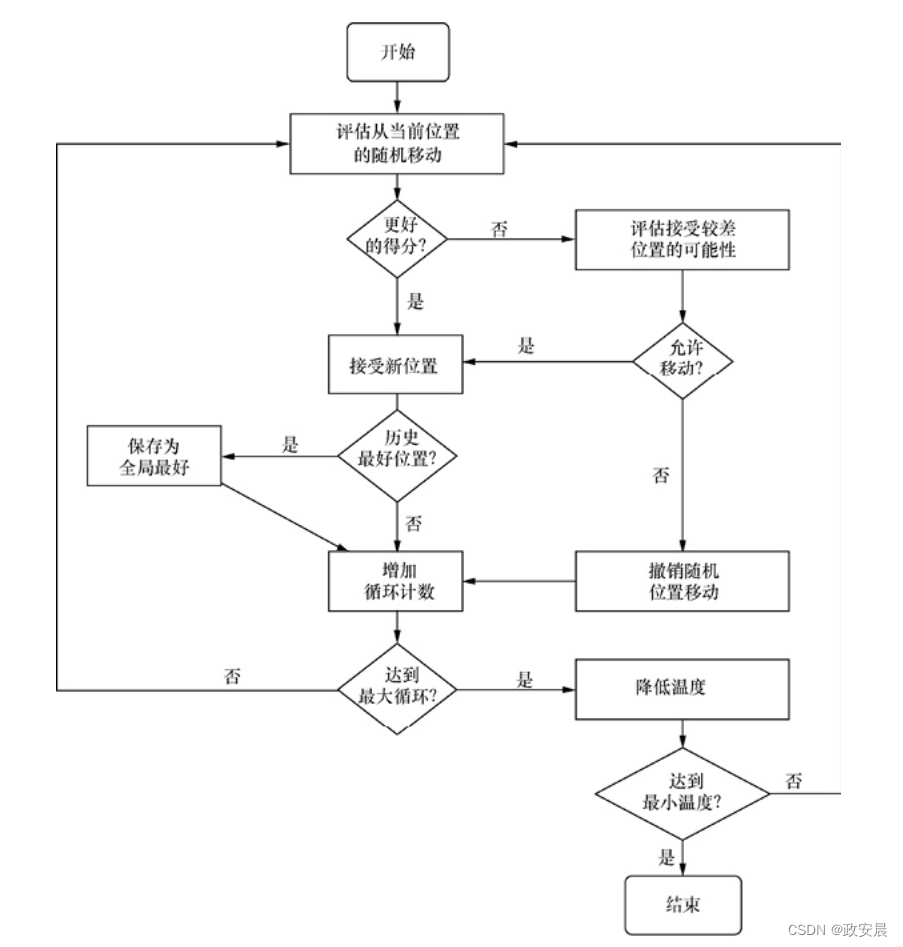
前馈神经网络可以利用模拟退火来学习鸢尾花数据集。以下程序展示了这种训练的输出:
Iteration #1, Score=0.3937, k=1,kMax=100,t=343.5891,prob=0.9998 Iteration #2, Score=0.3937, k=2,kMax=100,t=295.1336,prob=0.9997 Iteration #3, Score=0.3835, k=3,kMax=100,t=253.5118,prob=0.9989 Iteration #4, Score=0.3835, k=4,kMax=100,t=217.7597,prob=0.9988 Iteration #5, Score=0.3835, k=5,kMax=100,t=187.0496,prob=0.9997 Iteration #6, Score=0.3835, k=6,kMax=100,t=160.6705,prob=0.9997 Iteration #7, Score=0.3835, k=7,kMax=100,t=138.0116,prob=0.9996 ... Iteration #99, Score=0.1031, k=99,kMax=100,t=1.16E-4,prob= 2.8776E-7 Iteration #100, Score=0.1031, k=100,kMax=100,t=9.9999E-5,prob= 2.1443E-70 Final score: 0.1031 [0.22222222222222213, 0.6249999999999999, 0.06779661016949151, 0.04166666666666667] -> Iris-setosa, Ideal: Iris-setosa [0.1666666666666668, 0.41666666666666663, 0.06779661016949151, 0.04166666666666667] -> Iris-setosa, Ideal: Iris-setosa ... [0.6666666666666666, 0.41666666666666663, 0.711864406779661, 0.9166666666666666] -> Iris-virginica, Ideal: Iris-virginica [0.5555555555555555, 0.20833333333333331, 0.6779661016949152, 0.75] -> Iris-virginica, Ideal: Iris-virginica [0.611111111111111, 0.41666666666666663, 0.711864406779661, 0.7916666666666666] -> Iris-virginica, Ideal: Iris-virginica [0.5277777777777778, 0.5833333333333333, 0.7457627118644068, 0.9166666666666666] -> Iris-virginica, Ideal: Iris-virginica [0.44444444444444453, 0.41666666666666663, 0.6949152542372881, 0.7083333333333334] -> Iris-virginica, Ideal: Iris-virginica [1.178018083703488, 16.66575553359515, -0.6101619300462806, -3.9894606091020965, 13.989551673146842, -8.87489712462323, 8.027287801488647, -4.615098285283519, 6.426489182215509, -1.4672962642199618, 4.136699061975335, 4.20036115439746, 0.9052469139543605, -2.8923515248132063, -4.733219252086315, 18.6497884912826, 2.5459600552510895, -5.618872440836617, 4.638827606092005, 0.8887726364890928, 8.730809901357286, -6.4963370793479545, -6.4003385330186795, -11.820235441582424, -3.29494170904095, -1.5320936828139837, 0.1094081633203249, 0.26353076268018827, 3.935780218339343, 0.8881280604852664, -5.048729642423418, 8.288232057956957, -14.686080237582006, 3.058305829324875, -2.4144038920292608, 21.76633883966702, 12.151853576801647, -3.6372061664901416, 6.28253174293219, -4.209863472970308, 0.8614258660906541, -9.382012074551428, -3.346419915864691, -0.6326977049713416, 2.1391118323593203, 0.44832732990560714, 6.853600355726914, 2.8210824313745957, 1.3901883615737192, -5.962068350552335, 0.502596306917136]
最初的随机神经网络,多类对数损失得分很高,即30。随着训练的进行,该值一直下降,直到足够低时训练停止。对于这个例子,一旦错误降至10以下,训练就会停止。
要确定错误的良好停止点,你应该评估神经网络在预期用途下的运行情况。
低于0.5的对数损失通常在可接受的范围内;
但是,神经网络可能无法对所有数据集都达到这个得分。
 Elvis运算符(?:))





笔记)








)



