Squeeze-and-Excitation Networks
- 摘要
- 引言
- 什么是全局平均池化?
- 相关工作
- Deep architectures
- Squeeze-and-Excitation Blocks
- 3.1. Squeeze: Global Information Embedding
- 3.2. Excitation: Adaptive Recalibration
- 3.3. Exemplars: SE-Inception and SE-ResNet
- 5. Implementation
摘要
卷积神经网络建立在卷积运算的基础上,通过在局部感受野内融合空间信息和通道信息来提取信息特征。
为了提高网络的表示能力,最近的几种方法显示了增强空间编码的好处。
作者专注于通道关系,并提出了一种新的架构单元,称之为“挤压-激励”(SE)块,该单元通过明确建模通道之间的相互依赖性,自适应地重新校准通道级别(channel-wise )的特征响应。
作者证明,通过将这些块堆叠在一起所构建的 SENet 架构,在具有挑战性的数据集上泛化得非常好。至关重要的是,作者发现 SE 块以最小的额外计算成本为现有的最先进的深度体系结构带来了显著的性能改进。
引言
最近的工作表明,可以通过显式嵌入学习机制来提高网络的性能,这些学习机制有助于捕获空间相关性,而无需额外的监督。
其中一种方法是由 Inception 架构推广的,这表明网络可以通过在其模块中嵌入多尺度过程来实现竞争性精度。最近的研究试图更好地建模空间依赖性并纳入空间注意力。
在本文中,作者研究了结构设计的另一个方面——通道关系,通过引入一个新的结构单元,称之为“挤压和激发”(SE)块。目标是通过显式地建模其卷积特征通道之间的相互依赖性来提高网络的表示能力。
为了实现这一目标,提出了一种允许网络执行特征重新校准的机制,通过这种机制,网络可以学习使用全局信息来选择性地强调有用的特征并抑制不太有用的特征
任何给定的变换 F t r : X → U \textbf{F}_{tr} : \mathbf{X} \to \mathbf{U} Ftr:X→U, X ∈ R H ′ × W ′ × C ′ \mathbf{X} \in \mathbb{R}^{H' \times W' \times C'} X∈RH′×W′×C′, U ∈ R H × W × C \mathbf{U} \in \mathbb{R}^{H \times W \times C} U∈RH×W×C
可以构造一个相应的 SE 块来执行特征重新校准。
特征 U \mathbf{U} U 首先通过挤压操作,挤压操作将跨空间维度 H × W H × W H×W 的特征图聚合以生成通道描述符 (channel descriptor)。这个描述符嵌入了通道特征响应的全局分布,使来自网络的全局感受野的信息能够被其较低的层利用。随后是激励 (excitation)操作,其中通过基于通道依赖性的自门机制 (self-gating mechanism)为每个通道学习特定于样本的激活 (activations),控制每个通道的激励。然后将特征映射 U \mathbf{U} U 重新加权以生成 SE 块的输出,然后将其直接馈送到后续层。
什么是全局平均池化?
全局平均池化(Global Average Pooling, GAP)是一种在卷积神经网络中常用的池化技术,特别是在网络的最后几层。它的目的是将每个特征图(feature map)简化为一个单一的数值,从而减少模型的参数数量和计算复杂度。这在一定程度上有助于防止过拟合,并且使模型更易于解释。
在全局平均池化中,对于每个特征图,我们计算该特征图上所有元素的平均值,作为该特征图的代表值。如果我们有 C C C 个特征图,那么全局平均池化之后,我们将得到一个 1 × 1 × C 1 \times 1 \times C 1×1×C 的输出,其中每个通道的值都是对应特征图上所有元素的平均值。
全局平均池化会改变特征图的空间尺寸。无论输入特征图的尺寸是多少,全局平均池化都会将其压缩成 1 × 1 1 \times 1 1×1 的尺寸,但是保留通道数不变。这样做的好处是,它允许网络适应任何大小的输入图像,并且在将特征图转化为最终的分类预测时,减少了需要学习的参数数量。
总结来说,全局平均池化是一种将特征图的空间维度压缩到单个数值的技术,它确实会改变特征图的空间尺寸,并且常用于卷积神经网络的最后几层以简化模型并减少过拟合的风险。
如何理解上面这段话?
这段话介绍了Squeeze-and-Excitation (SE) block的基本工作原理,其中包含了几个关键概念:
Channel Descriptor(通道描述符):在SE block中,首先对特征图U进行“squeeze”操作,即通过全局平均池化(global average pooling)来聚合特征图的空间维度 H×W,从而产生一个通道描述符。这个描述符捕获了每个通道在整个空间范围内的全局分布情况。
Sample-specific activations(样本特定的激活值):指的是对于每个输入样本,SE block都会计算一组特定于该样本的激活值。这些激活值反映了在当前样本下,每个通道的重要性程度。
Excitation(激活):激活操作是SE block的核心,它根据每个通道的激活值来重新加权特征图U的每个通道。这样,网络可以根据当前输入样本的特征自适应地调整每个通道的重要性。
Self-gating mechanism(自门控机制):在“excitation”操作中,利用一种基于通道依赖性的自门控机制来学习每个通道的激活值。这种机制通常通过一个简单的全连接网络实现,网络的输入是通道描述符,输出是每个通道的激活值。
通过这种方式,SE block能够显式地建模通道间的依赖关系,并通过动态调整通道的重要性来增强网络的表示能力。
SE building block 的基本结构如图 1 1 1 所示
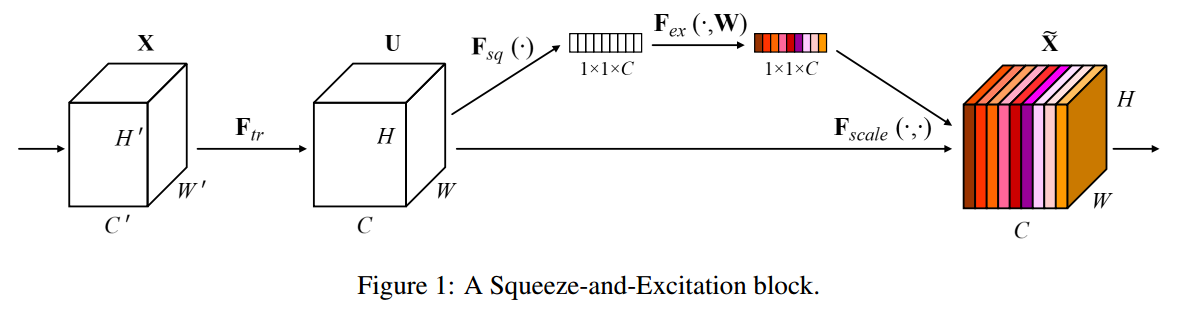
-
SE网络的构建:SE网络可以通过简单地堆叠一系列SE构建块(SE building blocks)来生成。这意味着你可以在网络的任何深度插入SE块,用它们替换原有的普通卷积块。
-
SE块在不同深度的作用:虽然SE块的基本结构是通用的,但它在网络不同深度的作用会根据网络的需要进行适应。
- 在早期层:SE 块学习以一种与类别无关的方式激活(excite)有信息量的特征,从而增强共享的低层表示的质量。这意味着在网络的初级阶段,SE 块帮助突出那些对于多个类别都有用的特征。
- 在后期层:SE 块变得越来越专门化,对不同的输入以高度特定于类别的方式做出响应。这意味着在网络的高层,SE 块能够针对特定的类别调整通道的重要性,从而提高网络对特定类别特征的敏感性。
-
特征重校准的累积效益:通过整个网络,SE 块进行的特征重校准(feature recalibration)的好处可以累积起来。这意味着 SE 块不仅在单个层中改善特征表示,而且还通过网络的深度增强了整体的表示能力。
开发新的 CNN 架构是一项具有挑战性的工程任务,通常涉及许多新的超参数和层配置的选择。
相比之下,上面概述的 SE 块的设计很简单,可以直接与现有的最先进的体系结构一起使用,这些体系结构的模块可以通过直接替换 SE 对应的模块来加强。
SE 块在计算上是轻量级的,只会略微增加模型复杂性和计算负担。
作者开发了几个 senet,并对 ImageNet 2012 数据集进行了广泛的评估。
为了证明它们的普遍适用性,作者还展示了 ImageNet 数据集之外的结果,表明所提出的方法并不局限于特定的数据集或任务。
相关工作
Deep architectures
跨通道关系:在传统的卷积神经网络中,跨通道的关系通常通过新的特征组合来建模,这些组合可以独立于空间结构(如使用 1 × 1 1×1 1×1 卷积)或与空间结构共同建模(使用标准卷积滤波器)。这些方法主要关注于减少模型和计算复杂度。
SE块的新思路:与上述方法不同,SE块提出了一种新的思路,即通过明确地建模通道间的动态非线性依赖关系来增强网络的表示能力。SE块利用全局信息(通过squeeze操作捕获)来指导每个通道的重要性(通过excitation操作实现),这有助于简化学习过程,并显著提高网络的表征能力。
总的来说,这段话强调了SE块相对于传统方法在建模通道间关系方面的创新和优势。
Squeeze-and-Excitation Blocks
Squeeze-and-Excitation block 是一个计算单元,可以为任何给定的变换构建:
F t r : X → U \textbf{F}_{tr} : \mathbf{X} \to \mathbf{U} Ftr:X→U, X ∈ R H ′ × W ′ × C ′ \mathbf{X} \in \mathbb{R}^{H' \times W' \times C'} X∈RH′×W′×C′, U ∈ R H × W × C \mathbf{U} \in \mathbb{R}^{H \times W \times C} U∈RH×W×C
为简单起见, 下面的符号中 F t r \textbf{F}_{tr} Ftr 是卷积算子
设 V = [ v 1 , v 2 , . . . , v C ] \mathbf{V} = [\textbf{v}_1, \textbf{v}_2, ..., \textbf{v}_C] V=[v1,v2,...,vC] 是学习到的卷积核的集合,
其中 v c \textbf{v}_c vc 表示第 c c c 个卷积滤波器的参数. 然后可以将 F t r \textbf{F}_{tr} Ftr 的输出写成
U = [ u 1 , u 2 , . . . , u C ] \mathbf{U} = [\textbf{u}_1, \textbf{u}_2, ..., \textbf{u}_C] U=[u1,u2,...,uC], 其中
u c = v c ∗ X = ∑ s = 1 C ′ v c s ∗ x s . \textbf{u}_c = \textbf{v}_c * \mathbf{X} = \sum_{s=1}^{C'} \textbf{v}_c^s * \textbf{x}^s. uc=vc∗X=s=1∑C′vcs∗xs.这里 ∗ * ∗ 表示卷积, v c = [ v c 1 , v c 2 , . . . , v c C ′ ] \textbf{v}_c = [\textbf{v}_c^1,\textbf{v}_c^2, ..., \textbf{v}_c^{C'}] vc=[vc1,vc2,...,vcC′] 和 X = [ x 1 , x 2 , . . . , x C ′ ] \mathbf{X} = [\textbf{x}^1, \textbf{x}^2, ..., \textbf{x}^{C'}] X=[x1,x2,...,xC′] (为了简化符号,省略了偏置项), 其中 v c s \textbf{v}_c^s vcs 是一个二维空间卷积核,表示 v c \textbf{v}_c vc 的单个通道,它作用于 X \mathbf{X} X 的相应通道。
由于输出是通过所有通道的求和产生的,因此通道依赖关系隐式嵌入在 v c \textbf{v}_c vc 中,但这些依赖关系与卷积滤波器捕获的空间相关性纠缠在一起。
目标是确保网络能够提高其对信息特征的敏感性,以便后续转换可以利用它们,并抑制不太有用的特征。
建议通过显式建模通道相互依赖性来实现这一目标,以便在将滤波器响应馈送到下一个变换之前,分两个步骤(挤压和激励)重新校准滤波器响应。图 1 1 1 显示了 SE 构建块的示意图。
3.1. Squeeze: Global Information Embedding
3.2. Excitation: Adaptive Recalibration
3.3. Exemplars: SE-Inception and SE-ResNet
5. Implementation
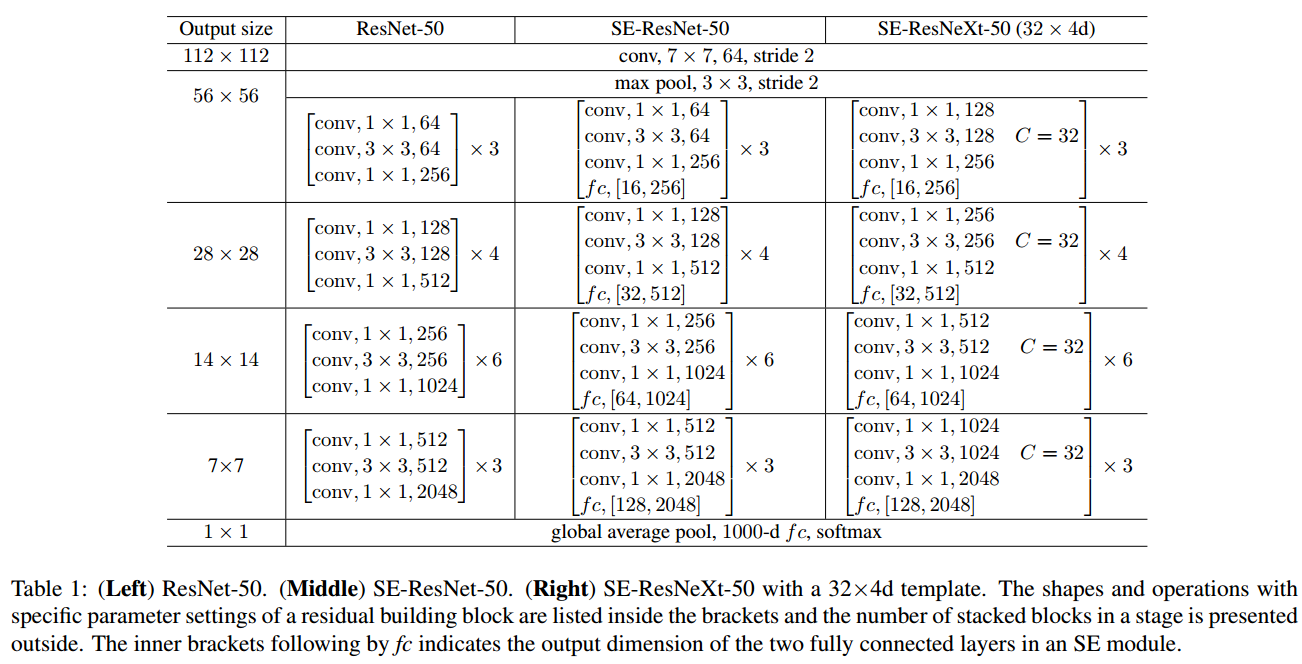
)

——朗道力学第一版序)


——filter、foearch、for in 、for of 、for的区别以及返回值)










:全局事件总线、消息订阅与发布pubsub、TodoList的编辑功能、$nextTick、过渡与动画)

—最近的一些面试汇总)
![[医学分割大模型系列] (3) SAM-Med3D 分割大模型详解](http://pic.xiahunao.cn/[医学分割大模型系列] (3) SAM-Med3D 分割大模型详解)