二、什么是 SimPy？

        SimPy 是一个开源 Python 库，专为建模和模拟离散事件系统而设计。它提供了用于创建模拟的构建块，使您能够准确地对系统中的时间和事件流进行建模。与变量随时间连续变化的连续模拟不同，离散事件模拟关注在特定时间点发生的事件。这些事件会触发系统中的状态变化，使 SimPy 特别适合涉及离散且通常不可预测的事件的建模过程。

SimPy 的一些主要功能包括：

1. 进程：在 SimPy 中，模拟中的实体表示为进程。这些进程可以是任何事物，例如队列中的人、交通网络中的车辆或计算机系统中的任务。您可以使用 Python 生成器函数定义流程，从而轻松建模复杂的异步行为。
2. 事件：事件是 SimPy 建模方法的核心。事件可以安排在特定时间或满足特定条件后发生。您可以创建事件链并通过调度事件来触发系统中的更改来管理模拟中的时间流。
3. 资源：在许多模拟中，资源是有限的，需要在不同实体之间共享。SimPy 提供了一个资源类，允许您对资源分配和争用进行建模。这对于数据中心服务器分配或工厂机器分配等建模场景非常有价值。
4. 统计和数据收集： SimPy 提供了一系列用于在模拟过程中收集数据的工具。这包括监视事件、跟踪实体在各种状态下花费的时间以及记录其他相关信息。这些统计数据对于分析和理解系统行为至关重要。
5. 集成： SimPy 与其他 Python 库和工具高度兼容。您可以将其与 NumPy 和 Pandas 等数据分析库结合使用来分析模拟结果并做出数据驱动的决策。

三、SymPy — 安装

        SymPy 有一个重要的必备库，名为mpmath。它是一个用于任意精度的实际复杂浮点运算的 Python 库。但是，当安装 SymPy 时，Python 的包安装程序 PIP 会自动安装它，如下所示 -

pip install sympy

import sympy
sympy.__version__Output:
'1.12'

四、SymPy — 符号计算

        符号计算涉及创建旨在操纵数学表达式和各种数学实体的算法。它融合了数学和计算机科学领域，通过使用数学符号来解析数学表达式。计算机代数系统 (CAS)，如 SymPy，通过利用传统手动技术中使用的符号来精确评估代数表达式。为了说明这一点，请考虑通过 Python 的数学模块计算数字的平方根，如下所示 -

import math 
print (math.sqrt(25), math.sqrt(7))Output:
5.0 2.6457513110645907

        您可能会发现此处显示了 7 的平方根的近似计算。但是，在 SymPy 中，默认情况下不计算缺乏完美平方根的数字的平方根，如下所示：

import sympy 
print (sympy.sqrt(7))Output:
sqrt(7)

        可以使用下面的代码片段以符号方式简化和显示表达式结果 -

import math
print (math.sqrt(12))Output:
3.4641016151377544

        您需要使用下面的代码片段来使用 sympy 执行相同的操作 -

print (sympy.sqrt(12))Output:
2*sqrt(3)

        在 Jupyter 笔记本中执行时，SymPy 代码利用 MathJax 库以 LaTeX 格式显示数学符号。以下代码摘录对此进行了演示：

from sympy import * 
x=Symbol ('x') 
expr = integrate(x**x, x) 
expr

在 python shell 中执行上述命令时，将生成以下输出 -

Integral(x**x, x)

这相当于

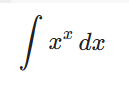
        非完美平方的平方根可以用 Latex 使用传统符号表示如下 -

from sympy import * 
x=7 
sqrt(x)

        上述代码片段的输出如下 -

        像 SymPy 这样的符号计算系统可以执行各种符号计算，包括求导数、积分和极限、求解方程以及使用矩阵等操作。SymPy 包包含各种模块，可实现绘图、渲染（例如，以 LATEX 格式）、物理、统计、组合学、数论、几何、逻辑等领域的符号运算。

五、SymPy — 数字

        SymPy 包中的核心模块包含表示原子序数的 Number 类。该类有两个子类：Float 类和 Rational 类。Rational 类由 Integer 类进一步扩展。

        Float 类表示任意精度的浮点数。

from sympy import Float 
Float(6.32)Output:
6.32

        SymPy 可以将整数或字符串转换为浮点数。

Float(10)Output:
10.0

Float('1.33E5')# scientific notationOutput:
133000.0

转换为浮点数时，还可以指定精度位数，如下所示 -

Float(1.33333,2)Output:
1.3

数字 (p/q) 的表示被表示为 Rational 类的对象，其中 q 是非零数字。

Rational(3/4)Output:
3
-
4

如果将浮点数传递给 Rational() 构造函数，它将返回其二进制表示形式的基础值

Rational(0.2)

为了更简单的表示，请指定分母限制。

Rational(0.2).limit_denominator(100)Output:
1
-
5

当您提供一个字符串作为 Rational() 构造函数的参数时，它会生成一个具有无限精度的有理数。

Rational("3.65")Output:
73
--
20

当提供两个数值参数时也可以创建有理对象，其属性包括分子和分母分量。

a=Rational(3,5) 
print (a) 
print ("numerator:{}, denominator:{}".format(a.p, a.q))Output:
3/5numerator:3, denominator:5

        SymPy 引入了 RealNumber 类，充当 Float 的同义词。此外，SymPy 为 Zero 和 One 建立了单例类，可以分别使用 S.Zero 和 S.One 来访问它们，如下所示。

S.ZeroOutput:
0

其他预定义的 Singleton 数字对象有 Half、NaN、Infinity 和 ImaginaryUnit

from sympy import S 
print (S.Half)Output:
1/2

Infinity 可用作 oo 符号对象或 S.Infinity

from sympy import oo 
oo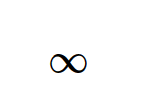

ImaginaryUnit 数字可以作为 I 符号导入或作为 S.ImaginaryUnit 访问，表示 -1 的平方根

from sympy import I 
IOutput:
i

from sympy import sqrt 
i=sqrt(-1) 
i*iOutput:
When you execute the above code snippet, you get the following output −-1

六、SymPy — 符号

        Symbol 类在 symPy 库中具有极其重要的意义。如前所述，符号计算围绕符号的使用展开。SymPy 变量本质上是 Symbols 类的实例。

        当您使用 Symbol() 函数时，它的参数应该是一个字符串，表示可以分配给变量的符号。

from sympy import Symbola = Symbol('a')
b = Symbol('b')
expression = a**3 + b**2
expression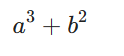

s=Symbol('side') 
s**3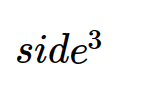

SymPy 提供了一个方便的 Symbols() 函数，可以同时声明多个符号变量。这些变量名称在字符串中指定，以逗号或空格分隔。

from sympy import symbols 
x,y,z=symbols("x,y,z")

        在 SymPy 库中，abc 模块包含所有拉丁字母和希腊字母，将它们视为符号。因此，这种方法提供了一种单独创建 Symbol 对象的便捷替代方法，从而简化了流程。

from sympy.abc import x,y,z

然而，值得注意的是，某些符号如 C、O、S、I、N、E 和 Q 已经被预定义。此外，abc 模块不包含具有多个字母的符号的定义。在这种情况下，您应该使用前面演示的 Symbol 对象。abc 模块建立保留名称，可以识别默认 SymPy 命名空间内的冲突定义。具体来说，clash1 包含单字母符号，而clash2 包含可能与现有定义冲突的多字母符号。

from sympy.abc import _clash1, _clash2 
_clash1Output:
{'C': C, 'O': O, 'Q': Q, 'N': N, 'I': I, 'E': E, 'S': S}

_clash2Output:
{'beta': beta, 'zeta': zeta, 'gamma': gamma, 'pi': pi}

        可以使用类似于 range() 函数的语法来创建索引符号。使用冒号指定范围。范围的类型由冒号右侧的字符确定。如果该字符是数字，则其左侧的所有数字均被视为起始值（非负），右侧的所有数字均被视为比结束值大 1。

from sympy import symbols 
symbols('a:7')Output:
(a0, a1, a2, a3, a4, a5, a6)

symbols('mark(1:5)')Output:
(mark1, mark2, mark3, mark4)

七、SymPy — 替换

        使用数学表达式时的一项基本操作涉及替换。在 SymPy 中，使用 subs() 函数将第一个参数的每个实例替换为第二个参数。

from sympy import sin, cos
from sympy.abc import x, aexpr = sin(x) * sin(x) + cos(x) * cos(x)
expr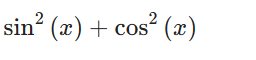

当我们需要评估特定的数学表达式时，这个函数被证明是有价值的。例如，当我们旨在通过将变量“a”替换为值 5 来确定给定表达式的结果时。

expr=a*a+2*a+5 
expr

expr.subs(a,5)Output:
40

from sympy.abc import x 
from sympy import sin, pi 
expr=sin(x) 
expr1=expr.subs(x,pi) 
expr1Output:
0

此函数还可以用于将一个子表达式替换为另一个子表达式。在给定的示例中，“b”被替换为“a+b”。

from sympy.abc import a,b 
expr=(a+b)**2 
expr1=expr.subs(b,a+b) 
expr1

八、SymPy — sympify() 函数

        sympify() 函数的目的是将任意表达式转换为与 SymPy 兼容的格式，从而允许其用作 SymPy 表达式。它能够将常规 Python 对象（例如整数）转换为 SymPy 对应对象。此外，即使是表示数字或数学表达式的字符串等对象也可以转换为 SymPy 表达式。

from sympy import sympify
expr="x**2+3*x+2" 
expr1=sympify(expr) 
expr1 
expr1.subs(x,2)Output:
12

        您可以将任何 Python 对象转换为 SymPy 对象，但需要注意的是，这种转换依赖于内部 eval() 函数的使用。因此，必须小心以确保输入表达式得到正确的清理。如果不这样做可能会导致引发 SympifyError。

sympify("x***2")

        当尝试执行表达式“x***2”的符号化由于引发异常而失败时，会发生 SympifyError。

        sympify() 函数接受以下参数： * strict：默认设置为 False。当设置为 True 时，它​​只允许对具有显式定义转换的类型进行转换。否则，当遇到未定义的转换时，它会引发 SympifyError。*评估：当设置为False时，算术运算和运算符将转换为其SymPy等效项，而无需实际评估表达式。

sympify("10/5+4/2")Output:
4

sympify("10/5+4/2", evaluate=False)

九、SymPy — evalf() 函数

        该函数旨在计算指定的数值表达式，精度可达小数点后 100 位。此外，它接受一个“subs”参数，该参数应该是一个包含分配给符号变量的数值的字典。考虑以下表达式。

from sympy.abc import r 
expr=pi*r**2 
expr

        使用 evalf() 函数计算上面的表达式，并将“r”替换为值 5。

expr.evalf(subs={r:5})Output:
78.5398163397448

        默认浮点精度设置为 15 位小数，但可以通过指定高达 100 的精度值来更改。在这种特殊情况下，给定表达式的计算精度为 20 位小数。

expr=a/b 
expr.evalf(20, subs={a:100, b:3})Output:
33.333333333333333333

十、SymPy — Lambdify() 函数

        lambdify 函数用作将 SymPy 表达式转换为 Python 函数的方法。在需要计算广泛值的表达式的情况下，使用 evalf() 函数可能不是最有效的方法。Lambdify 函数的方式类似于 lambda 函数，并增加了将 SymPy 符号映射到指定数值库（通常是 NumPy）中相应符号的功能。默认情况下，lambdify 使用数学标准库来实现。

expr=1/sin(x) 
f=lambdify(x, expr) 
f(3.14)Output:
627.8831939138764

        在处理涉及多个变量的表达式时，您应该注意，在使用该lambdify()函数时，初始参数应该是包含这些变量的列表，并且后面应该是您要计算的表达式。

expr=a**2+b**2 
f=lambdify([a,b],expr) 
f(2,3)Output:
13

        尽管如此，为了利用 numpy 库作为计算后端的数值功能，我们必须将其指定为lambdaify() 函数的参数。

f=lambdify([a,b],expr, "numpy")

我们在上面的函数中使用两个 numpy 数组作为两个参数 a 和 b。对于 numpy 数组，执行时间相当快。

import numpy 
l1=numpy.arange(1,6) 
l2=numpy.arange(6,11) 
f(l1,l2)Output:
array([ 37, 53, 73, 97, 125], dtype=int32)

十一、SymPy — 逻辑表达式

        布尔函数是在 sympy.basic.booleanarg 模块中创建的。您可以使用标准 Python 运算符构建布尔语句，例如 & (And)、| （或）和 ~（非），以及 >> 和 <<。这些布尔表达式构建在 Basic 类之上，该类在 SymPy 的核心模块中定义。

        现在，我们来讨论一下BooleanTrue 函数。该函数相当于常规 Python 中的 True 值。当您调用它时，它会返回一个可以通过 S.true 访问的唯一实例。

例如，考虑以下代码：

from sympy import *
x = sympify(true)
x, S.trueOutput:
(True, True)

        在此代码中，我们创建一个变量x并为其赋值S.true，演示了 BooleanTrue 在 SymPy 中的使用。

        “BooleanFalse”函数在SymPy 库中充当 Python 中布尔 False 值的等效表示。要访问此功能，您可以使用符号“S.false”。

        以下是如何使用它的示例：

from sympy import * 
x = sy.symbols('false')  # Creating a symbol using S.false
x, S.falseOutput:
(False, False)

        在此代码中，我们使用 S.false 功能创建了一个符号“x”，它表示布尔 False 值。

        与函数

        逻辑 AND 函数通过评估其两个输入值进行运算，如果其中任何一个为 False，则产生 False 结果。该函数有效地模仿了“&”运算符的行为。

        以下是在 Python 中使用 SymPy 库的示例：

from sympy import symbols
from sympy.logic.boolalg import Andx, y = symbols('x y')
x = True
y = Trueresult = And(x, y)
symbolic_result = x & y# The 'result' and 'symbolic_result' variables both hold the value 'True'.Output:
(True, True)

        在此示例中，使用函数和符号“&”运算符执行逻辑 AND 运算And，产生 True 值，因为 'x' 和 'y' 都设置为 True。

y=False 
And(x,y), x"&"yOutput:
(False, False)

        或者函数

        该函数采用两个布尔值作为输入，如果其中至少一个为 True，则生成 True 结果。'|' 操作员可以方便地复制其功能。

from sympy import *
from sympy.logic.boolalg import Or
x, y = symbols('x y')
x = True
y = False
Or(x, y), x | yOutput:
(True, True)

x=False 
y=False 
Or(x,y), x|yOutput:
(False, False)

        不是功能

        当逻辑非函数应用于布尔参数时，会产生与输入值相反的值。换句话说，如果参数最初为 False，则生成 True；如果参数最初为 True，则生成 False。此否定操作也可以使用 ~ 运算符来实现，它执行相同的逻辑反转。下面提供了一个说明性示例：

from sympy import * 
from sympy.logic.boolalg import Or, And, Not 
x, y = symbols('x y') 
x = True 
y = False 
Not(x), Not(y)Output:
(False, True)

在此代码片段中，由于最初是原样Not(x)返回，并按最初原样返回。FalsexTrueNot(y)TrueyFalse

Not(And(x,y)), Not(Or(x,y))Output:
(True, False)

        异或函数

        当奇数个输入参数为 True，其余为 False 时，逻辑 XOR（异或）函数会产生 True 结果。相反，当偶数个输入参数为 True，其余为 False 时，它​​会产生 False 结果。使用 ^ 运算符时可以观察到相同的行为。

from sympy import * 
from sympy.logic.boolalg import Xor 
x,y=symbols('x y') 
x=True 
y=FalseXor(x,y), x^yOutput:
(True, True)

a,b,c,d,e=symbols('a b c d e') 
a,b,c,d,e=(True, False, True, True, False) 
Xor(a,b,c,d,e)Output:
True

        在前面的示例中，当三个参数（奇数）设置为 True 时，Xor 运算将产生 True 结果。相反，如果 True 参数的数量是偶数，则结果将为 False，如下所示 -

a,b,c,d,e=(True, False, False, True, False) 
Xor(a,b,c,d,e)Output:
False

        与非函数

        该函数执行逻辑 NAND 运算，评估其输入值，并在至少其中一个为 False 时生成 True，仅当所有输入值均为 True 时生成 False。

from sympy import * 
from sympy.logic.boolalg import Nand 
a,b,c=symbols('a b c') 
a,b,c=(True, False, True) 
Nand(a,b,c), Nand(a,c)Output:
(True, False)

        也没有功能

        该函数执行逻辑 NOR 运算，其中评估其输入，如果其中任何一个为 True，则产生 False 结果；如果实际上全部为 False，则产生 True。

from sympy import * 
from sympy.logic.boolalg import Nor 
a,b,c=symbols('a b c') 
a,b,c=(True, False, True) 
Nor(a,b,c), Nor(a,c)Output:
(False, False)

        值得注意的是，SymPy 提供了方便的运算符，例如“^”用于 Xor、“~”用于 Not、“|” Or 表示“&”，And 表示“&”，但在标准 Python 用法中，这些符号用作按位运算符。因此，如果将它们应用于整数，结果会有所不同。

        等效功能

        该函数产生等价关系。仅当 A 和 B 均为 true 或均为 false 时，它​​才会确认“Equivalent(A, B)”为 true。仅当所有给定参数在逻辑上相等时，它才提供真实结果，否则，它返回错误结果。

from sympy import * 
from sympy.logic.boolalg import Equivalent 
a,b,c=symbols('a b c') 
a,b,c=(True, False, True) 
Equivalent(a,b), Equivalent(a,c)Output:
(False, True)

        ITE功能

        该函数的功能类似于编程语言中的条件“If-Then-Else”语句。当您调用 ITE(A, B, C) 时，它会评估 A 的真值，如果 A 为真，则返回结果 B，否则返回结果 C。需要注意的是，所有参数都必须是布尔值。

from sympy import * 
from sympy.logic.boolalg import ITE 
a,b,c=symbols('a b c') 
a,b,c=(True, False, True) 
ITE(a,b,c), ITE(a,c,b)Output:
(False, True)

十二、SymPy — 查询

        SymPy 包包含假设模块，该模块提供了一组用于收集有关数学表达式的信息的工具。该模块引入了ask()函数，该函数的目的是提取此类信息。

sympy.assumptions.ask(property)

        以下属性提供有关表达式的有用信息 -

        代数(x)

        对于一个被认为是代数的数字，它应该满足一个关键条件：它必须作为具有非零系数且仅包含有理数的多项式方程的解。以 √2 为例，它属于代数，因为它是方程 x² — 2 = 0 的解，其中系数是有理数。

        复数(x)

        复数谓词。当且仅当 x 属于复数集合时才为真。

        复合材料(x)

        “ask(Q.composite(x))”函数仅当“x”是正整数并且除 1 和数字本身之外至少有一个正除数时，才会对给定值“x”产生真实结果，从而确认它确实是一个合数。

        偶数、奇数

        当 x 位于偶数集合和奇数集合中时，ask() 分别返回 true。

        假想

        该属性表示虚数谓词。如果 x 可以写为实数乘以虚数单位 I，则成立。

        整数

        Q.integer(x) 返回的此属性返回 true，表示 x 属于偶数集。

        理性的、非理性的

        当且仅当 x 是任何不能表示为整数比的实数时，Q.irrational(x) 才为 true。例如，pi 是一个无理数。

        正负

        检查数字是正数还是负数的谓词

        零、非零

        判断数字是否为零

from sympy import * 
x=Symbol('x') 
x=10 
ask(Q.algebraic(pi))
Falseask(Q.complex(5-4*I)), ask( Q.complex(100))
(True, True)x,y=symbols("x y") 
x,y=5,10 
ask(Q.composite(x)), ask(Q.composite(y))
(False, True)ask(Q.even(x)), ask(Q.even(y))
(False, True)x,y= 2*I, 4+5*I 
ask(Q.imaginary(x)), ask(Q.imaginary(y))
(True, False)x,y=5,10 
ask(Q.even(x)), ask(Q.even(y)), ask(Q.odd(x)), ask(Q.odd(y))
(False, True, True, False)x,y=5,-5 
ask(Q.positive(x)), ask(Q.negative(y)), ask(Q.positive(x)), ask(Q.negative(y))
(True, True, True, True)ask(Q.rational(pi)), ask(Q.irrational(S(2)/3))
(False, False)ask(Q.zero(oo)), ask(Q.nonzero(I))
(False, False)

结论 

        基础知识到此结束！！！展望未来，我们将深入研究用例和一些相当高级的功能。但是，嘿，不要忘记保存它，因为您需要像我一样重新访问它几次。请查看我的其他文章并关注我！快乐阅读。