
论文链接:http://anthology.aclweb.org/attachments/P/P18/P18-1012.Presentation.pdf
发表会议:ACL 2018
摘要
知识图谱的嵌入表示在近几年已经成为一个非常活跃的研究领域,众多相关方法相继被提出,这些嵌入方法是将知识图谱中的实体和关系表示成同一向量空间中的向量。虽然知识图谱的嵌入表示在各种任务中被广泛应用,但是对嵌入表示的几何理解尚未被探索,本文旨在填补这项空白。本文深入分析知识图谱嵌入表示的几何形状,并分析其与任务性能和其他超参数之间的关联。通过在真实数据集上进行广泛的实验,本文发现了一些值得注意的现象,例如不同类别的嵌入方法学习到的嵌入表示在几何形状上存在明显差异。
度量标准
1. ATM
ATM(alignment to mean)是指向量集合 V 中的一个向量 v 与平均向量的余弦相似度。
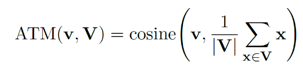
2. Conicity
Conicity是指向量集合 V 中所有向量 ATM 的平均值。
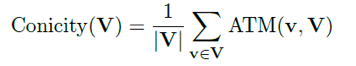
3. VS
VS(vector spread)是指向量集合V中所有向量ATM的方差。
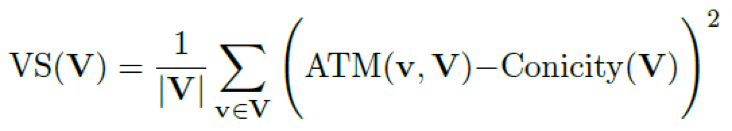
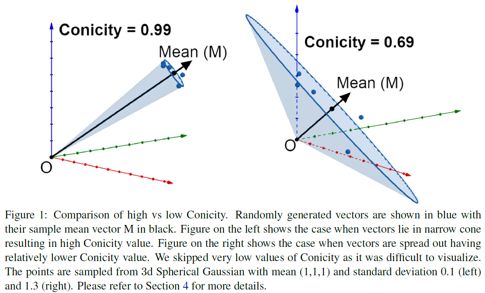
图1给出了一个实例来帮助理解这几个指标,图中是一个三维坐标系(展示的点是随机生成的),左图表示的是高锥度(conicity)和低向量分散度(VS)的情形,而右图表示的是低锥度和高向量分散度的情形。
4. AVL
AVL(average vector length)是指向量集合V中所有向量的平均长度( L_2范数)。
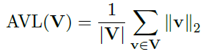
实验分析
本文的主要考虑6个知识图谱的嵌入表示模型,并把6个方法分为两类。一类是加法(additive)模型,有TransE[2]、TransR[3]和STransE[4];另一类是乘法(multiplicative)模型,有DistMult[5]、HolE[6]和ComplEx[7]。同时,本文采用了两个常见数据集FB15K和WN18。本文主要从以下4个发现展开实验分析。
1. 模型类型对几何形状的影响
不同模型在实体向量的几何形状上存在明显差异。乘法模型的ATM值均为正值且向量分散度较低。加法模型此形成鲜明对比,加法模型的ATM值正负皆有且分布较为均衡,同时向量分散度较高。这说明乘法模型得到的嵌入向量不是均匀的分散在向量空间中,而加法模型得到的嵌入向量则是均匀的分散在向量空间中。
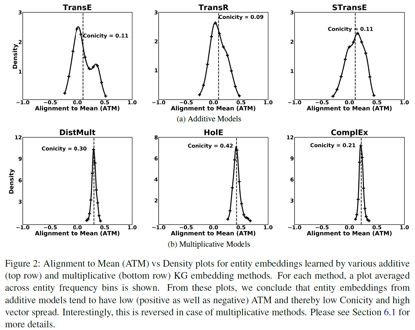
2. 反例数量对几何形状的影响
乘法模型的锥度(conicity)随着反例数量的增加而增大,而加法模型的锥度对反例数量不敏感。在平均向量长度(AVL)方面,乘法模型中的DistMult和ComplEx随着反例数量的增加而减小,HolE则几乎没有变化,这是因为HolE把实体向量限制在了单位球内。所有加法模型的AVL也对反例数量不敏感,而它们也有和HolE类似的限制。
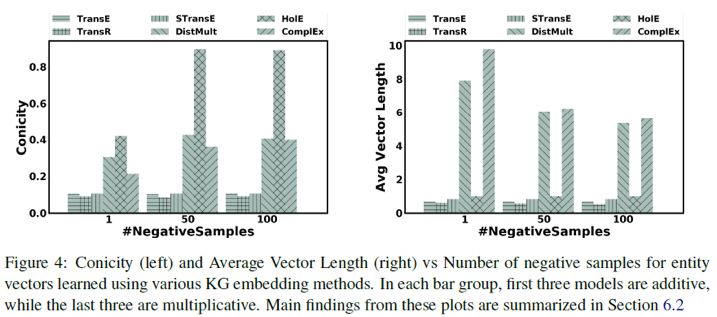
3. 向量维数对几何形状的影响
随着向量维数的增加,乘法模型的锥度呈现出下降的趋势,而平均向量长度则呈现出上升趋势。加法模型的锥度和平均向量长度则对向量维数不敏感。
4. 几何形状与性能的联系
本实验以链接预测任务为例,采用与TransE相同的实验设定。当反例数量相同时,锥度小的乘法模型的性能更优;当反例数量增加时,乘法模型表现更好。加法模型的性能与锥度并无太大关系。在平均向量长度方面,对于除HolE之外的乘法模型而言,当反例数量一定时,平均向量长度越大性能越好;而对于加法模型和HolE而言,平均向量长度与性能的关系并不显著,这个现象是由于这些方法使用单位向量长度来限制嵌入向量所导致的。

参考
[1] Chandrahas, Aditya Sharma, Partha Talukdar: Towards Understanding the Geometry of Knowledge Graph Embeddings. ACL 2018: 122-131.
[2] Antoine Bordes, Nicolas Usunier, Alberto Garciaduran, Jason Weston, Oksana Yakhnenko: Translating Embeddings for Modeling Multi-relational Data. NIPS 2013: 2787-2795.
[3] Yankai Lin, Zhiyuan Liu, Maosong Sun, Yang Liu, Xuan Zhu: Learning entity and relation embeddings for knowledge graph completion. AAAI 2015: 2181-2187.
[4] Dat Quoc Nguyen, Kairit Sirts, Lizhen Qu, Mark Johnson: STransE: anovel embedding model of entities and relationships in knowledge bases.NAACL-HLT 2016: 460-466.
[5] Bishan Yang, Wentau Yih, Xiaodong He, Jianfeng Gao, Li Deng: Embedding Entities and Relations for Learning and Inference in Knowledge Bases. ICLR2015.
[6] Maximilian Nickel, Lorenzo Rosasco, Tomaso Poggio: Holographic embeddings of knowledge graphs. AAAI 2016: 1955-1961.
[7] Theo Trouillon, Johannes Welbl, Sebastian Riedel, Eric Gaussier, Guillaume Bouchard: Complex embeddings for simple link prediction. ICML 2016: 2071-2080.
OpenKG.CN
中文开放知识图谱(简称OpenKG.CN)旨在促进中文知识图谱数据的开放与互联,促进知识图谱和语义技术的普及和广泛应用。

转载须知:转载需注明来源“OpenKG.CN”、作者及原文链接。如需修改标题,请注明原标题。
点击阅读原文,进入 OpenKG 博客。








)


)







)