作者 | 陈东阳博士 仿真秀科普作者

一、柱体结构涡激振动定义
对于海洋工程、风工程上普遍采用的圆柱形断面结构物,流体绕过柱体时会产生交替发放的泻涡,这种交替发放的泻涡又会在柱体上生成顺流向及横流向周期性变化的脉动压力。
如果此时柱体是弹性支撑的,或者柔性管体允许发生弹性变形,那么脉动流体力将引发柱体(管体)的周期性振动,这种规律性的柱状体振动反过来又会改变其尾流的泻涡发放形态。这种流体-结构物相互作用的问题被称作"涡激振动"(Vortex-Induced Vibration :VIV),它是典型的一种流固耦合振动现象。
二、柱体结构涡激振动动力学模型及仿真方法简介
进行二维弹性支撑柱体的数值模拟是研究海洋工程和风工程中柱体结构涡激振动现象和机理的重要手段。
根据牛顿第二定律,2-DOF弹性支撑的柱体运动的控制方程可以写为:
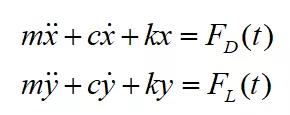
(1)
式中, m为圆柱体的质量, c为结构阻尼系数, k为结构刚度系数。
式(1)又可以写为:
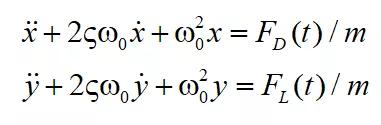
(2)
式(2)中,柱体固有频率
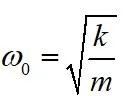
,
阻尼比
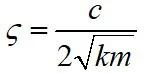
对于涡激振动的数值模拟大多以柱体的横向振动研究为主,同时考虑横向和来流向的耦合振动研究相对较少。其主要原因在于,对柱体结构涡激振动数值模拟,必须保证柱体周围网格质量非常好,才能有效预测涡激振动响应。
一般使用网格质量高的结构化网格,但是当柱体结构发生较大振动位移时,周围流场网格会发生畸变,甚至产生负网格,导致计算失败。如果再考虑流向耦合振动,计算难度将非常大,计算成功率也将明显降低。
如果采用非结构化网格,且采用网格重构技术,可以吸收柱体较大的振动位移,但是非结构化网格质量相比结构化网格质量较差,且采用非结构化网格必定需要大大增加网格量,从而大大增加了计算时间。
此外,如果对于涡激振动抑制装置设计研究,也就是在柱体结构表面形状变复杂的情况下,网格划分难度和计算难度也将大大增加。因此,寻求一种既可以保证网格质量,又能不大幅度增加网格数量,且可以避免网格畸变或者负网格问题的方法十分重要。
基于CFD商业软件FLUENT和结构动力学原理,通过用户自定义函数(UDF)及嵌套网格技术,建立了2-DOF弹性支撑柱体结构VIV数值模型。非定常不可压缩流体RANS方程为:
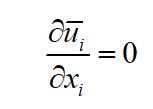
(4)
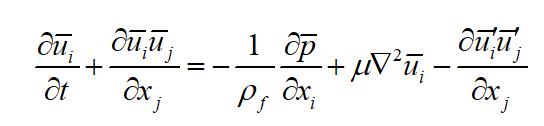
(5)
式(5)中,
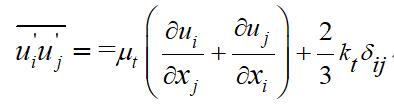
式中,
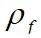
为不可压缩流体的密度;
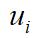
表示
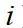
方向上的瞬时速度分量,
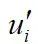
为
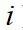
方向上速度脉动量,
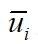
为速度的时间平均值;

分别表示笛卡尔坐标系、时间、压力、运动粘度;
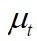
为湍流黏度,下标“t”表示湍流;
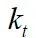
为湍动能;
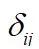
是“Kronecker delta”符号,就是当
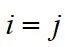
时,
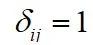
,当
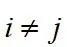
时,
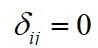
。湍流模型选用SST k–ω湍流模型。通过计算流场,可以得到二维柱体表面的压力分布,进而可以得到作用在二维柱体上的升力和阻力系数:
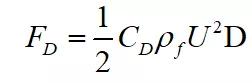
(6)
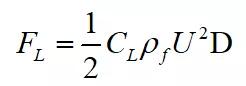
(7)
结合方程(2),2-DOF弹性支撑的柱体运动的控制方程可以写为:
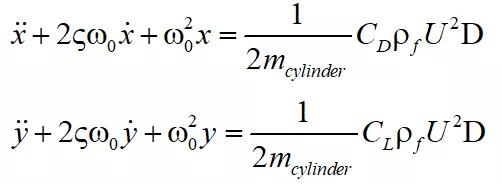
(8)
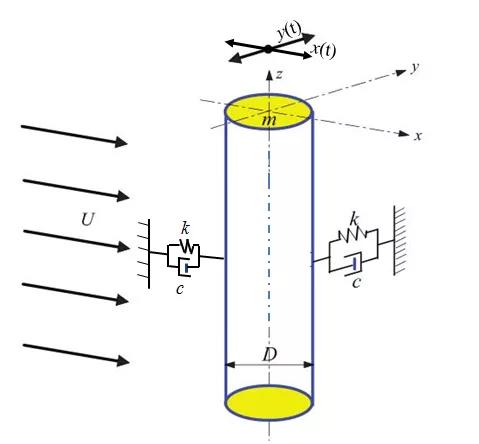
(a) 两自由度弹性支撑刚性柱体
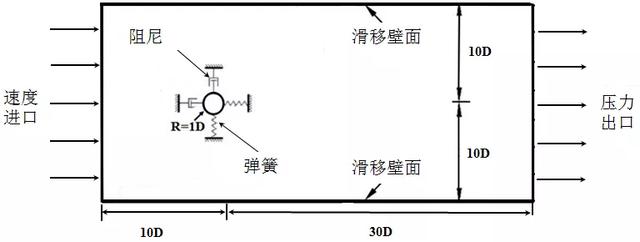
(b) 二维两自由度弹性支撑刚性柱体VIV模型
图1 2-DOF弹性支撑圆柱体VIV模型示意图
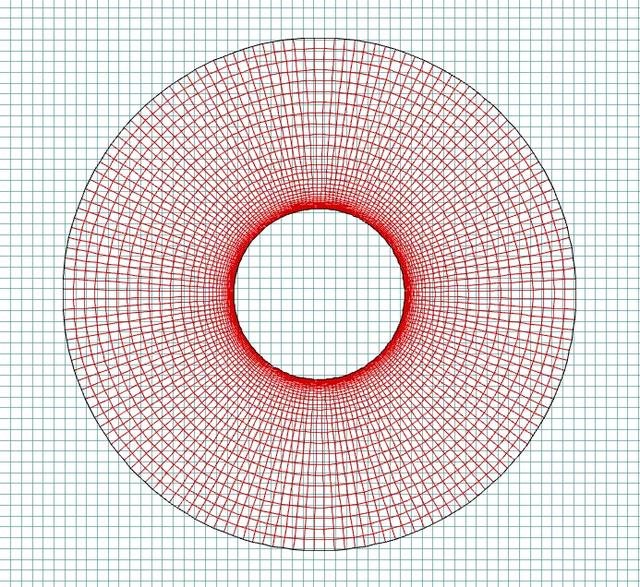
(a) 背景网格与嵌套网格
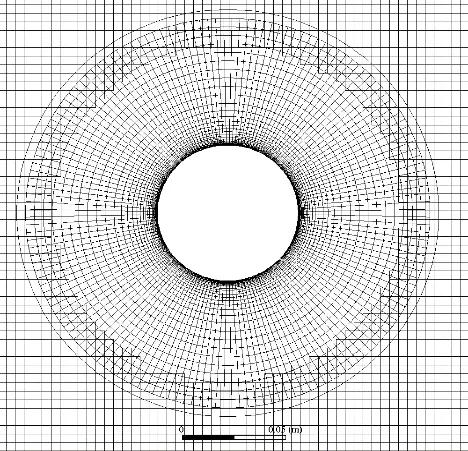
(b) 挖洞和插值
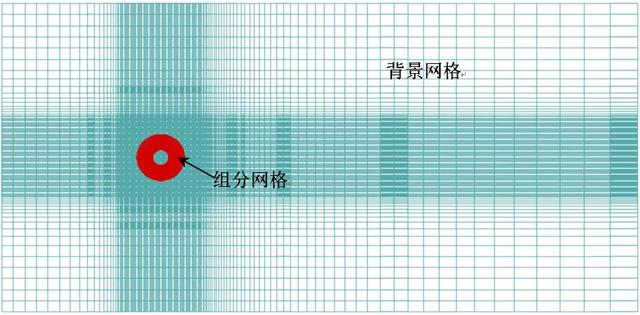
(c) 整个流体域的网格
图2 2-DOF弹性支撑圆柱体流场计算网格
两自由度弹性支撑刚性柱体在流体作用下的结构示意图如图1(a)所示,二维2-DOF振动柱体VIV模型示意图如图1(b)所示。一般柱体流场的尾迹区域需要大于等于22.5D(D为柱体直径),整体局域高度一般需要大于等于20D,柱体振动才不受流体区域边界的影响。
因此,综合考虑计算条件的情况下,流场域的尺寸大小如图1(b)中标注所示,尾迹区域30D,柱体前端和上下距离柱体都是10D。包围这柱体的组分网格外边界直径大小为3D。流场入口边界条件为速度入口,出口为压力出口,上下壁面为滑移壁面,柱体表面即动边界为无滑移壁面。
流场随着柱体边界的改变而改变,通过动网格技术来实现流场中柱体边界的运动。嵌套网格技术是最新的动网格技术,主要适用于刚性边界运动问题。如图2所示,流场域网格划分采用的是嵌套网格。如图2(a)所示,背景网格和嵌套网格都使用结构化网格,靠近柱体表面部分为边界层网格(
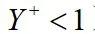
),较好的保证了网格质量。
采用嵌套网格技术,可以无需担心网格畸变以及负网格导致求解失败等问题。同时,不会较多的增加计算量。嵌套网格即多重网格相互重叠组合成的一组网格。有可能存在两套或者两套以上的网格相互重叠。
嵌套网格求解的大致思路为:首先划分包裹柱体的组分网格(组分网格数量为5262),和外流场的背景网格(背景网格数量为15731),求解器识别嵌套网格边界,对被组分网格遮蔽的背景网格部分进行“挖洞”,然后对嵌套区域边界单元进行插值,将背景区域的边界单元变量信息插值到嵌套区域的边界单元(如图2(b)所示),最后进行流场计算。整个流场的计算网格如图2(c)所示。
对于流场的数值计算,时间项采用全隐式积分方法,对流项则采用二阶迎风离散格式。控制方程中速度分量与压力的耦合则采用COUPLED算法进行处理。初始条件为
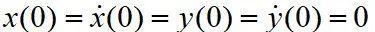
。
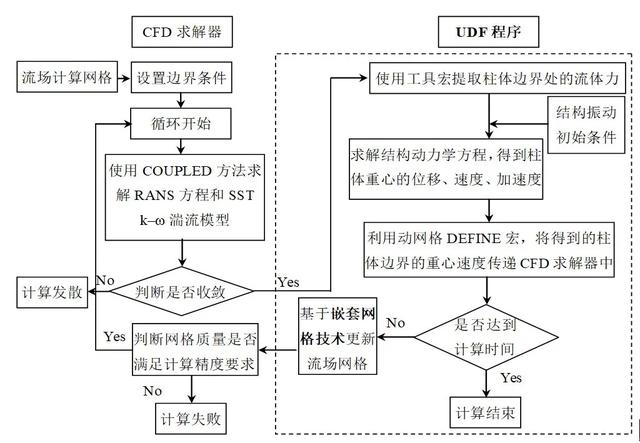
图3 2-DOF弹性支撑圆柱体VIV计算流程图
流场域求解基于CFD商业软件FLUENT,根据边界条件获得流场和二维柱体表面的压力、速度等信息。提取作用在柱体表面的力,然后代入柱体的结构运动方程,通过求解二维柱体的运动方程,得到当前时间步长下的柱体运动的位移和速度。同时利用得到的柱体位移和瞬时速度,更新流场网格,然后进行下一个时间步的计算。这个双向流固耦合仿真过程是通过FLUENT软件的用户自定义函数(UDF)来实现的。
UDF中可以使用标准C语言的库函数,也可使用FLUENT中预定义的宏。通过预定义宏可以获得FLUENT计算过程中的流场数据。FLUENT中用户自定义函数是通过DEFINE宏来实现的。基于CFD的2-DOF弹性支撑柱体VIV数值求解的计算流程图如图3所示。图中的虚线框内为通过C语言编制的UDF程序来实现。
三、部分仿真结果展示
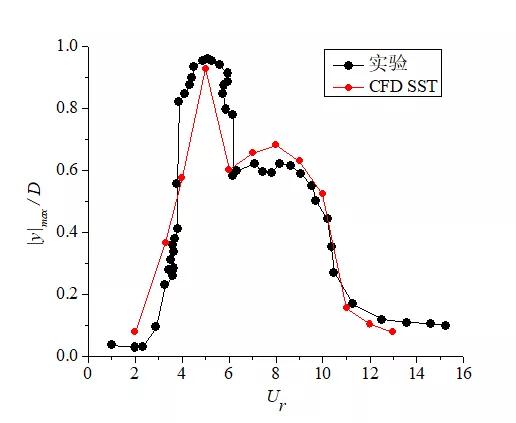
(a)不同约化速度下的振幅分布
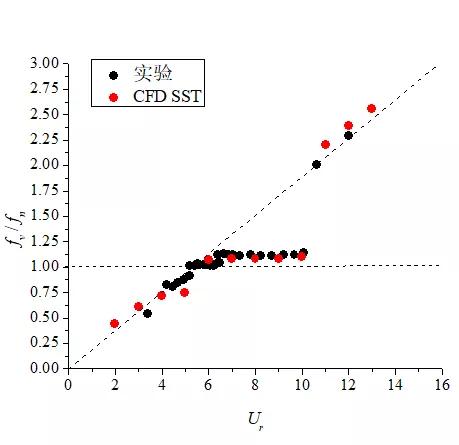
(b)频率比随约化速度变化图
图4 基于CFD模型的2-DOF柱体VIV计算结果
柱体涡激振动的最大幅值及频率比随不同约化速度的变化如图4所示,与实验数据对比,误差较小,验证了本文计算方法的正确性。
从图4(a)可以看出,数值仿真出3种响应分支,在
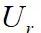
=3~4之间的时候,原始分支向上端分支转变;当
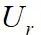
=5~6之间的时候,出现下端分支。在上端分支中振幅达到最大值0.98,而在下端分支中振幅最大值0.642;从
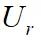
=11的时候开始,圆柱体的响应位移又回落到一个很小的数值。
从图4(b)可以看出,在频率“锁定”区间
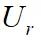
=4~10内,柱体的实际振动频率
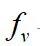
与固定柱体的泄涡频率
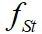
分离,不再符合
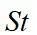
与Re数关系图。同时,柱体的实际涡泻频率
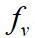
与柱体固有频率
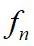
比值稳定在1.15附近,而在解锁区域,柱体的实际振动频率
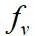
与固定柱体的涡脱频率
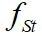
相同,这与前人的实验结果大致相同。
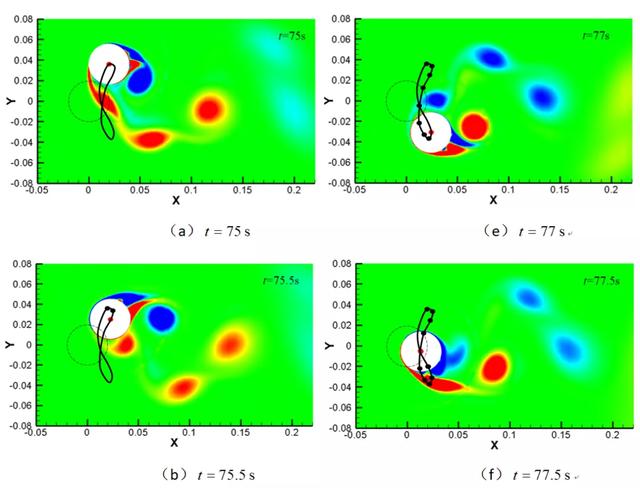
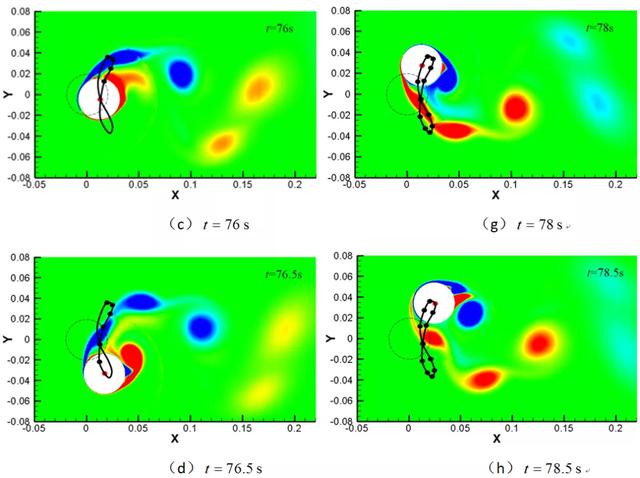
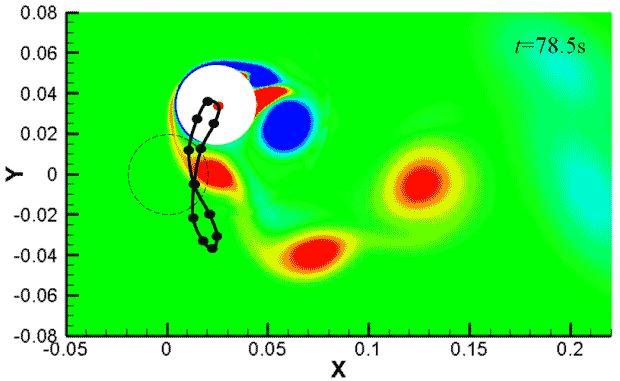
图5 时,不同时刻的涡量云图(周期T=3.34s)
图5给出了
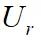
=5时弹性支撑柱体的75s~78.5s的涡量云图,包含了一个周期的运动,从图中可以看出,
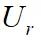
=5时的涡脱模式为P+S模式(即一个涡脱周期内有一个单个涡+一对涡形成)。
Govardhan 和 Williamson 的实验研究表明一般在柱体振幅较大时候涡脱模式为P+S或者2P(即在一个涡脱周期内有2对尾涡形成),在振幅较小的时候涡脱模式为2S(即在一个涡脱周期内有2个单独的尾涡形成)。图5中的黑虚线为柱体的原始位置,红点为柱体当前时刻的中心位置,从图中可以看出,柱体振动游走的轨迹是一个“8”字形。
四、基于ANSYS FLUENT的流固耦合仿真教程20讲
以上是ANSYS FLUENT流固耦合仿真教程中的柱体结构涡激振动仿真案例。自2020年4月,我在仿真秀官网/App同时发布了一套精品课《FLUENT 流固耦合方法与技能 20讲》掌握ANSYS流固耦合仿真方法和关键技巧。当前已经更新10期。
限时特价(限20名)
限时优惠:399元(价值:499 元 )
课程永久保存,随时回放,可开具发票
讲师提供vip群学习答疑和模型下载
课程安排:

作者:陈东阳博士 仿真秀专栏作者

进入直播间观看《Fluent 流固耦合方法与技能20讲》






)

)






)



![.Net下二进制形式的文件(图片)的存储与读取 [ZT]](http://pic.xiahunao.cn/.Net下二进制形式的文件(图片)的存储与读取 [ZT])