【每日算法】基数排序算法

1）算法简介

基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。基数排序的发明可以追溯到1887年赫尔曼·何乐礼在打孔卡片制表机（Tabulation Machine）上的贡献。

2）算法描述和分析

整个算法过程描述如下：
1、将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。
2、从最低位开始，依次进行一次排序。
3、这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。

基数排序的时间复杂度是 O(k•n)，其中n是排序元素个数，k是数字位数。

注意这不是说这个时间复杂度一定优于O(n·log(n))，因为k的大小一般会受到n的影响。以排序n个不同整数来举例，假定这些整数以B为底，这样每位数都有B个不同的数字，k就一定不小于logB(n)。由于有B个不同的数字，所以就需要B个不同的桶，在每一轮比较的时候都需要平均n·log2(B) 次比较来把整数放到合适的桶中去，所以就有：k 大于或等于 logB(n)
每一轮(平均)需要 n·log2(B) 次比较

所以，基数排序的平均时间T就是：
T ≥ logB(n)·n·log2(B) = log2(n)·logB(2)·n·log2(B) = log2(n)·n·logB(2)·log2(B) = n·log2(n)

所以和比较排序相似，基数排序需要的比较次数：T ≥ n·log2(n)。故其时间复杂度为 Ω(n·log2(n)) = Ω(n·log n) 。

3）算法图解、flash演示、视频演示

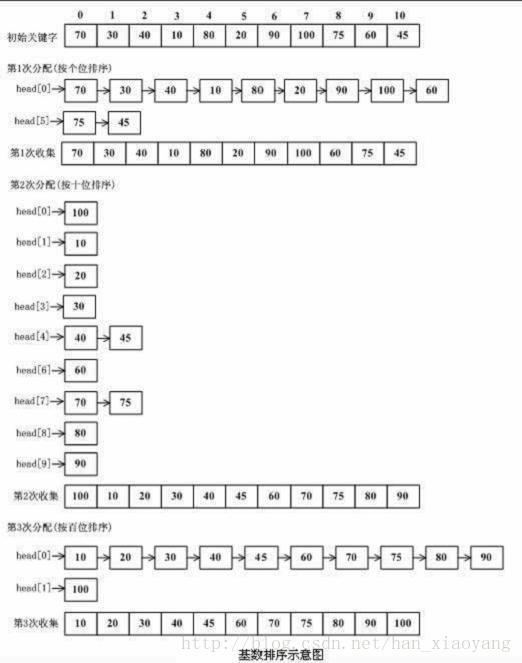
图解：
基数排序

Flash：
可参见http://ds.fzu.edu.cn/fine/resources/FlashContent.asp?id=91中的flash过程

视频：
http://www.tudou.com/programs/view/vfoUHC-tgi0

4）算法代码

#include <stdio.h>   
#include <stdlib.h>   
void radixSort(int data[]) {  int temp[10][10] = {0};   int order[10] = {0};   int n = 1;   while(n <= 10) {   int i;  for(i = 0; i < 10; i++) {   int lsd = ((data[i] / n) % 10);   temp[lsd][order[lsd]] = data[i];   order[lsd]++;   }   // 重新排列  int k = 0;  for(i = 0; i < 10; i++) {   if(order[i] != 0)  {  int j;  for(j = 0; j < order[i]; j++, k++) {   data[k] = temp[i][j];   }   }  order[i] = 0;   }   n *= 10;   }       
}  
int main(void) {   int data[10] = {73, 22, 93, 43, 55, 14, 28, 65, 39, 81};   printf("\n排序前: ");   int i;  for(i = 0; i < 10; i++)   printf("%d ", data[i]);   putchar('\n');   radixSort(data);  printf("\n排序後: ");   for(i = 0; i < 10; i++)   printf("%d ", data[i]);   return 0;   
}