定义

一幅图像可看成由两部分组成，即

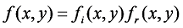
• fi代表随空间位置不同的亮度（Illumination）分量，其特点是缓慢变化，集中在图像的低频部分。
• fr代表景物反射到人眼的反射（Reflectance）分量，其特点包含了景物各种信息，高频成分丰富。

上式为同态滤波模型公式，其中，
0 < i ( x , y ) < 无 穷

和
0 < r ( x , y ) < 1

入射分量可以在0-无穷之间变化，反射分量只能在0-1之间变化，当反射分量为0时，说明物体将光全吸收，为黑色，当反射分量为1时，说明物体将光全反射，为白色。

同态滤波流程

同态滤波过程，分为以下5个基本步骤：

• 取对数
  
• 取对数结果做傅里叶变换
  
• 设计一个实中心对称的频域滤波器H(u,v)，与上步傅里叶变换结果阵列相乘
• 傅里叶反变换，返回到空域
• 取指数，得空域滤波结果。

方框图表示如下：

可以看出同态滤波的关键在于同态滤波器H(u,v)的设计，同态滤波的目的在于：对一幅光照不均匀的图像，适当压制亮度分量，增强反射分量，以此来实现亮度调整与对比度提升，从而改善图像的视觉质量。

通过以上分析我们可以知道：同态滤波器可以由高通滤波器来实现，但是又不能完全截断低频成分，只要适当压低即可，所以同态滤波器的函数表示如下：

$$其中，yL<1,yH>1，控制滤波器幅度的范围。Hhp通常为高通滤波器，如高斯（Gaussian）高通滤波器、巴特沃兹(Butterworth)高通滤波器、Laplacian滤波器等。$$
如高通滤波器采用高斯高通滤波器则有如下形式：

同态滤波器对应的图像表示如下：

其中， c为一个常数，控制滤波器形态，从低频到高频的斜率，c越大，斜坡带越陡峭

matlab实现代码

注意：取指数后一定要进行像素拉伸

%读入图片
img = imread('office.png');
img = rgb2gray(img);
figure(1);
subplot(2, 1, 1);
imshow(img);
title('Raw Image');
gamma_H = 2;
gamma_L = 0.25;
c = 0.25;
D0 =100;
f = double(img);
f = log(f + 1);%取指数
F = fft2(f);%傅里叶变换
F=fftshift(F);%频谱搬移
[height, width] = size(F);
%设计一个同态滤波器
H = HomomorphicFiltering(gamma_H, gamma_L, c, D0, height, width);
g=H.*F;%同态滤波
g = ifft2(ifftshift(g));%频谱搬移,傅里叶逆变换
g = exp(g)-1;
g = real(g);
%拉伸像素值
new_img = Expand(g);
subplot(2,1,2);
imshow(new_img);
title('Homomorphic Filtered Image(D0 = 100)');function new_img = Expand( img ) [height, width] = size(img);max_pixel = max(max(img));min_pixel = min(min(img));new_img=zeros(height,width);for i = 1 : heightfor j = 1 : widthnew_img(i, j) = 255 * (img(i, j) - min_pixel) / (max_pixel - min_pixel);endendnew_img = uint8(new_img);
endfunction H = HomomorphicFiltering( gamma_H, gamma_L, c, D0, height, width )for i = 1 : heightx = i - (height / 2);for j = 1 : widthy = j - (width / 2);H(i, j) = (gamma_H - gamma_L) * (1 - exp(-c * ((x ^ 2 + y ^ 2) / D0 ^ 2))) + gamma_L;endend
end

运行结果

参考链接

图像的同态滤波原理及实现