
some quoted by
Fundebug:代码面试需要知道的8种数据结构(附面试题及答案链接)zhuanlan.zhihu.com
added with other sources
8 种常用数据结构
- 数组
- 栈
- 队列
- 链表
- 图
- 树
- 哈希表
- priorityqueue

1. 数组
数组(Array)大概是最简单,也是最常用的数据结构了。其他数据结构,比如栈和队列都是由数组衍生出来的。
下图展示了 1 个数组,它有 4 个元素:
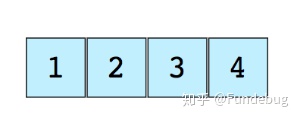
每一个数组元素的位置由数字编号,称为下标或者索引(index)。大多数编程语言的数组第一个元素的下标是 0。
根据维度区分,有 2 种不同的数组:
- 一维数组(如上图所示)
- 多维数组(数组的元素为数组)

2. 栈
撤回,即 Ctrl+Z,是我们最常见的操作之一,大多数应用都会支持这个功能。你知道它是怎么实现的吗?答案是这样的:把之前的应用状态(限制个数)保存到内存中,最近的状态放到第一个。这时,我们需要栈(stack)来实现这个功能。
栈中的元素采用 LIFO (Last In First Out),即后进先出。
下图的栈有 3 个元素,3 在最上面,因此它会被第一个移除:


3. 队列
队列(Queue)与栈类似,都是采用线性结构存储数据。它们的区别在于,栈采用 LIFO 方式,而队列采用先进先出,即FIFO(First in First Out)。
下图展示了一个队列,1 是最上面的元素,它会被第一个移除:



4. 链表
链表(Linked List)也是线性结构,它与数组看起来非常像,但是它们的内存分配方式、内部结构和插入删除操作方式都不一样。
链表是一系列节点组成的链,每一个节点保存了数据以及指向下一个节点的指针。链表头指针指向第一个节点,如果链表为空,则头指针为空或者为 null。
链表可以用来实现文件系统、哈希表和邻接表。
下图展示了一个链表,它有 3 个节点:

链表分为 2 种:
- 单向链表
- 双向链表

Time Complexity:
- Indexing: Linked Lists: O(n)
- Search: Linked Lists: O(n)
- Optimized Search: Linked Lists: O(n)
- Insertion: Linked Lists: O(1)
5. 图
图(graph)由多个节点(vertex)构成,节点之间阔以互相连接组成一个网络。(x, y)表示一条边(edge),它表示节点 x 与 y 相连。边可能会有权值(weight/cost)。

图分为两种:
- 无向图
- 有向图
在编程语言中,图有可能有以下两种形式表示:
- 邻接矩阵(Adjacency Matrix)
- 邻接表(Adjacency List)
遍历图有两周算法
- 广度优先搜索(Breadth First Search)
- 深度优先搜索(Depth First Search)

6. 树
树(Tree)是一个分层的数据结构,由节点和连接节点的边组成。树是一种特殊的图,它与图最大的区别是没有循环。
树被广泛应用在人工智能和一些复杂算法中,用来提供高效的存储结构。
下图是一个简单的树以及与树相关的术语:
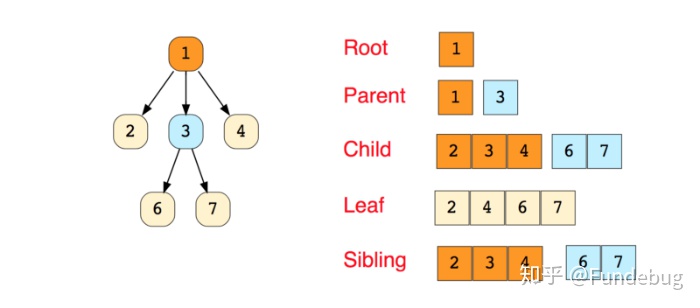
树有很多分类:
- N 叉树(N-ary Tree)
- 平衡树(Balanced Tree)
- 二叉树(Binary Tree)
- 二叉查找树(Binary Search Tree)
- 平衡二叉树(AVL Tree)
- 红黑树(Red Black Tree)
- 2-3 树(2–3 Tree)
其中,二叉树和二叉查找树是最常用的树。

Time Complexity:
- Indexing: Binary Search Tree: O(log n)
- Search: Binary Search Tree: O(log n)
- Insertion: Binary Search Tree: O(log n)
7. 哈希表
哈希(Hash)将某个对象变换为唯一标识符,该标识符通常用一个短的随机字母和数字组成的字符串来代表。哈希可以用来实现各种数据结构,其中最常用的就是哈希表(hash table)。
哈希表通常由数组实现。
哈希表的性能取决于 3 个指标:
- 哈希函数
- 哈希表的大小
- 哈希冲突处理方式
下图展示了有数组实现的哈希表,数组的下标即为哈希值,由哈希函数计算,作为哈希表的键(key),而数组中保存的数据即为值(value):


TreeMap
TreeMap can be a bit handy when we only need to store unique elements in a sorted order. Java.util.TreeMap uses ared-black treein the background which makes sure that there are no duplicates; additionally it also maintains the elements in a sorted order.
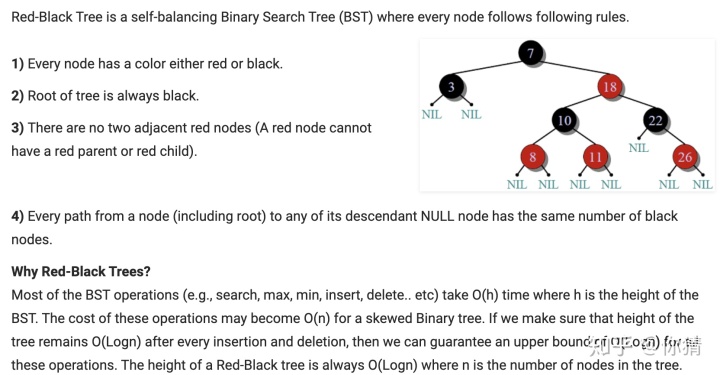
8. PriorityQueue













. 这里用flip()有什么作用?这是反转缓冲区的方法,好像用不上。...)






