🎈 算法并不一定都是很难的题目，也有很多只是一些代码技巧，多进行一些算法题目的练习，可以帮助我们开阔解题思路，提升我们的逻辑思维能力，也可以将一些算法思维结合到业务代码的编写思考中。简而言之，平时进行的算法习题练习带给我们的好处一定是不少的，所以让我们一起来养成算法练习的习惯。今天练习的题目是一道比较简单的题目 ->公交站间的距离

问题描述

环形公交路线上有 n 个站，按次序从 0 到 n - 1 进行编号。我们已知每一对相邻公交站之间的距离，distance[i] 表示编号为 i 的车站和编号为 (i + 1) % n 的车站之间的距离。

环线上的公交车都可以按顺时针和逆时针的方向行驶。

返回乘客从出发点 start 到目的地 destination 之间的最短距离。

示例 1：

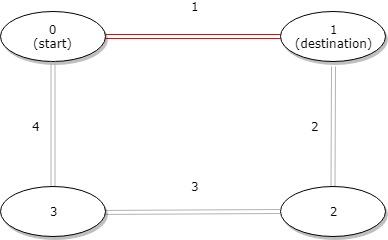
输入： distance = [1,2,3,4], start = 0, destination = 1
输出： 1
解释： 公交站 0 和 1 之间的距离是 1 或 9，最小值是 1。

示例 2：

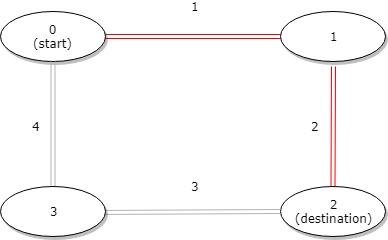
输入： distance = [1,2,3,4], start = 0, destination = 2
输出： 3
解释： 公交站 0 和 2 之间的距离是 3 或 7，最小值是 3。

示例 3：

输入： distance = [1,2,3,4], start = 0, destination = 3
输出： 4
解释： 公交站 0 和 3 之间的距离是 6 或 4，最小值是 4。

提示：

• 1 <= n <= 10^4
• distance.length == n
• 0 <= start, destination < n
• 0 <= distance[i] <= 10^4

思路分析

首先我们要先理解一下题目的意思，公交路线为一个环形，题目会给我们一个数组distance，每一对相邻公交站之间的距离，distance[i] 表示编号为 i 的车站和编号为 (i + 1) % n 的车站之间的距离。因为公交路线为一个环形，所以我们只能按照顺时针或逆时针方向驶向相邻的公交车站，也就是说编号为i的公交站只能驶向编号为(i + 1) % n 或 (i - 1 + n) % n。所以从start驶向destination只有两条路线，我们只需要分别算出两条路线的行驶距离，取较小的即可。

• 1、先算环形路线总距离

我们可以使用reduce方法来快速求出数组的和：

const sum = distance.reduce((a, b) => a + b);

• 2、顺时针从start驶向destination的距离

首先我们可以先保证start 小于 destination：if (start > destination) [start, destination] = [destination, start];，然后遍历对start和destination之间的数据进行求和即可：

if (start > destination) [start, destination] = [destination, start];
let res = 0;
while (start < destination) {res += distance[start++];
}

• 3、计算逆时针方向路线距离并取其较小值

前面我们已经计算出环形路线的总和了，所以我们可以直接使用总和减去当前路线的距离，即可得出另一路线的距离：

return Math.min(res, sum - res);

AC代码

完整AC代码如下：

/*** @param {number[]} distance* @param {number} start* @param {number} destination* @return {number}*/
var distanceBetweenBusStops = function (distance, start, destination) {const sum = distance.reduce((a, b) => a + b);if (start > destination) [start, destination] = [destination, start];let res = 0;while (start < destination) {res += distance[start++];}return Math.min(res, sum - res);
};

当然，我们也可以通过一次遍历的方法来直接得出答案：

var distanceBetweenBusStops = function (distance, start, destination) {if (start > destination) [start, destination] = [destination, start];let sum1 = 0,sum2 = 0;distance.forEach((item, index) => {if (index >= start && index < destination) sum1 += item;else sum2 += item;});return Math.min(sum1, sum2);
};

公众号

关注公众号『前端也能这么有趣』，获取更多有趣内容。

说在后面

🎉 这里是 JYeontu，现在是一名前端工程师，有空会刷刷算法题，平时喜欢打羽毛球 🏸 ，平时也喜欢写些东西，既为自己记录 📋，也希望可以对大家有那么一丢丢的帮助，写的不好望多多谅解 🙇，写错的地方望指出，定会认真改进 😊，偶尔也会在自己的公众号『前端也能这么有趣』发一些比较有趣的文章，有兴趣的也可以关注下。在此谢谢大家的支持，我们下文再见 🙌。