04730电子技术基础 · 语雀(完全笔记)
电阻元件、电感元件和电容元件的概念、伏安关系,以及功率分析是我们以后分析电 路的基础知识。
电阻元件
电阻及其与温度的关系
电阻
电阻元件是对电流呈现阻碍作用的耗能元件,例如灯泡、电热炉等电器。
计算公式为:

式中,ρ为制成电阻的材料电阻率,国际单位为欧姆·米(Ωꞏ m);l 为绕制成电阻的导线长度,国际单位为米(m);S 为绕制成电阻的导线横截面积,国际单位为平方米(m^2 );R 为电阻值,国际单位为欧姆(Ω)。
电阻与温度的关系
电阻元件的电阻值大小一般与温度有关,衡量电阻受温度影 响程度的物理量是温度系数,其定义为温度每升高 1℃ 时电阻值发生变化的百分数。
如果设任一电阻元件在温度 t1时的电阻值为 R1,当温度升高到 t2时电阻值为 R2,则该 电阻在 t1 ~ t2温度范围内的(平均)温度系数为

如果 R2 > R1,则α > 0,将 R 称为正温度系数电阻,即电阻值随着温度的升高而增大;
如果 R2< R1,则α < 0,将 R 称为负温度系数电阻,即电阻值随着温度的升高而减小。
显然 α 的绝对值越大,表明电阻受温度的影响也越大。
![]()
线性电阻
定义
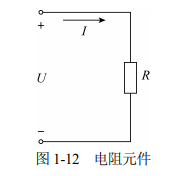
任何一个二端元件,若选取元件电压 U 与电流 I 方向关联,即方向一致, 如图 1-12 所示,在任意时刻的电压和电流之间存在代数关系,即不论电压和电流的波形如 何,电阻元件的伏安关系服从欧姆定律
![]()
式中,G = 1/R,电阻 R 的倒数 G 叫作电导,其国际单位为西门子(S),则此二端元件称为电阻元件,单位为欧姆(Ω)。
伏安特性曲线
线性电阻元件的伏安特性曲线是一、三象限的一条过原点的直线,如图 1-13 所示。

短路和开路
短路:短路(U=0)可看成电阻为零的电阻元件,其特性曲线与 I 轴重合。
开路:开路(I=0)可看成电阻为无穷大的电阻元件,其特性曲线与 U 轴重合 。
功率
对于任意线性电阻,若选取元件或电路部分的电压 u 与电流 i 方向关联,即方向一致,因为 R=u(t)/ i(t) ,因此 p(t) = u(t)i(t) >0,也就是说,这种电阻元件始终吸收功率,为耗能元件。
电阻(或其他的电路元件)上吸收的能量与时间区间相关。设从 t0到 t 时间区间内电阻 R 吸收的能量为 w(t),则该能量应等于从 t0到 t 对电阻吸收的功率 p(t)做积分,即
![]()
(自己尝试下进行公式推导,便于理解)
结论:无论电流、电压如何变化,电阻上的功率 P 总是大于零,说明电阻总是在消耗功率,电阻是耗能元件。
电容元件
电容器
结构
两个彼此靠近又相互绝缘的导体就构成了一个电容器,这对导体叫电容器的两个极板。
种类
电容器按其电容量是否可变,可分为固定电容器和可变电容器,可变电容器还包括半可变电容器。固定电容器的电容量是固定不变的,它的性能和用途与两极板间的介质有关。一般常用的介质有云母、陶瓷、金属氧化膜、纸介质、铝电解质等。
电解电容器是有正负极之分的,使用时不可将极性接反或接到交流电路中,否则会将电解电容器击穿
电容量在一定范围内可调的电容器叫可变电容器。半可变电容器又叫微调电容器。
作用
电容器是储存和容纳电荷的装置,也是储存电场能量的装置。电容器每个极板上所储存的电荷的量叫电容器的电量。
将电容器两极板分别接到电源的正负极上,使电容器两极板分别带上等量异号电荷, 这个过程叫电容器的充电过程。
电容器充电后,极板间有电场和电压。
用一根导线将电容器两极板相连,两极板上正负电荷中和,电容器失去电量,这个过 程称为电容器的放电过程。
平行板电容器
由两块相互平行、靠得很近、彼此绝缘的金属板所组成的电容器 叫平行板电容器。平行板电容器是一种最简单的电容器。
线性电容
定义
任何一个二端元件,如果在任意时刻的电压和电流之间的关系总可以由 q - u 平面上的一条过原点的曲线所决定,则此二端元件称为电容元件。数学定义式为
![]()
元件图形符号
元件图形符号如图 1-14 所示,图中电压与电流为关联参考方向。
线性电容的库伏特性曲线
线性电容元件的库伏特性曲线是一、三象限的一条过 原点的直线,如图 1-15 所示。

电容 C 表征元件储存电荷的能力,对于极板电容而言,其大小不随电路情况变化,取决于介电常数、极板相对的面积及极板间距。

线性电容的伏安特性
由于 i=dq/dt,而q=Cu ,所以电容的伏安(u- i)关系为微分关系,即i=C(du/dt) 。由此可见,电路中流过电容的电流的大小与其两端的电压的变化率成 正比,电压变化越快,电流越大。可以得出结论:电容元件隔直通交,通高阻低。

由此可见,电容元件某一时刻的电压不仅与该时刻流过电容的电流有关,还与初始时 刻的电压大小有关。可见,电容是一种电压“记忆”元件。
功率
对于任意线性的正值电容,若选取元件或电路部分的电压 u 与电流 i 方向关 联,即方向一致,则其功率为
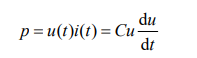
那么从 t0 到t 时间内,电容元件吸收的电能为
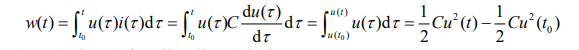
则从 t1到 t2 时间内,电容元件吸收的电能为
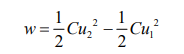
(判定电容元件充放电公式)
也就是说,当 u2>u1时, w >0 ,电容吸收能量,为充电过程;当 u2<u1 时, w < 0, 电容放出能量,为放电过程。
说明以下几点
① 电容为储能元件,并不消耗电能。
② 电容为电压记忆元件,其电压与初始值有关。
③ 电容为动态元件,其电压、电流为积分关系。
④ 电容为电压惯性元件,即电流为有限值时,电压不能跃变。
⑤ 电容元件隔直通交,通高阻低。
电容器的连接包括串联和并联
① 电容器的串联
把几个电容器首尾相接连成一个无分支的电路,称为电容器的串 联,如图 1-16 所示。
串联时,每个极板上的电荷量都是 q。设每个电容器的电容分别为 C1、C2、C3,电压 分别为 U1、U2、U3,则

即串联电容器总电容的倒数等于各电容器电容的倒数之和。
② 电容器的并联
如图 1-17 所示,把几个电容器的一端连在一起,另一端也连在一 起的连接方式叫作电容器的并联。

电容器并联时,加在每个电容器上的电压都相等。设电容器的电容分别为 C1、C2、C3, 所带的电量分别为 q1、q2、q3,则

设并联电容器的总电容(等效电容)为 C,由 q = CU 得C=C1+C2+C3 ,即并联电容器的总电容等于各个电容器的电容之和。
电容器中的电场能量。
① 能量来源
电容器在充电过程中,两极板上有电荷积累,极板间形成电场。电场 具有能量,此能量是从电源吸取过来储存在电容器中的。
② 储能大小的计算
电容器充电时,极板上的电荷量 q 逐渐增加,两板间电压 uC也 在逐渐增加,电压与电荷量成正比,即 q = Cu,在电压、电流关联参考方向下,功率为

式中,电容 C 的单位为 F,电压 uC的单位为 V,电荷量 q 的单位为 C,能量的单位为 J。
电容器中储存的能量与电容器的电容成正比,与电容器两极板间电压的平方成正比。
电容器在电路中的作用
当电容器两端电压增加时,电容器从电源吸收能量并储 存起来;当电容器两端电压降低时,电容器便把它原来所储存的能量释放出来。即电容器 本身只与电源进行能量交换,而并不损耗能量,因此电容器是一种储能元件。
实际的电容器由于介质漏电及其他原因,也要消耗一些能量,使电容器发热,这种 量消耗称为电容器的损耗。
电容器质量的判别
利用电容器的充放电作用,可用万用表的电阻挡来判别较大容量电容器的质量(此质量意为:品质度量,非物理中的质量)。(怕大家不晓得电阻档,找了一张图片,大家也可以买一个万用表玩玩,毕竟后面要考实践,指不定要用的)

将万用表的表棒分别与电容器的两端接触,若指针偏转后又很快回到接近起始位置的地方,则说明电容器的质量很好,漏电很小;若指针回不到起始位置,停在标度盘某处,说明电容器漏电严重,这时指针所指的电阻数值即该电容的漏电阻值;若指针偏转到零欧位置后不再回去,说明电容器内部短路;若指针根本不偏转,则说明电容器内部可能断路。
电感元件
定义
任何一个二端元件,如果在任意时刻的电压和电流之间的关系总可以由自感磁通链-电 流(ψ - i)平面上的一条过原点的曲线所决定,则此二端元件称为电感元件。数学定义式为
![]()
式中,Ψ 为通过线圈的磁链,Ψ =NΦ,单位是韦伯(Wb);I 为通过线圈的电流,单位是安培(A);L 为比例常数,称为线圈的电感或自感系数,简称自感,体现电感线圈储存磁场的能力,单位是亨利(H)。
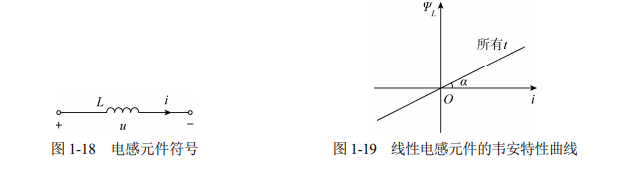
元件符号与图形
电感元件符号与图形如图 1-18 所示。
线性电感元件的韦安特性曲线
线性电感元件的韦安特性曲线是一、三象限的一条过原点的直线,如图 1-19 所示。
线性电感的伏安特性

由此可见,电感元件某一时刻流过的电流不仅与该时刻电感两端的电压有关,还与初始时刻的电流大小有关。可见,电感是一种电流“记忆”元件。
功率
对于任意线性的正值电感,若选取元件或电路部分的电压 u 与电流 i 方向关联,其功率为

说明
(1) 电感为储能元件,并不消耗电能。
(2) 电感为电流记忆元件,其电流与初始值有关。
(3) 电感为动态元件,其电流、电压为积分关系。
(4) 电感为电流惯性元件,即电压为有限值时,电流不能跃变。
(5) 电感元件通直隔交,通低阻高。(这里要与电容元件做个对比)
-Part.04 基础环境配置)




)





)




)


