一、前言:
这是怀化学院的:Java数据结构中的一道难度偏难的一道编程题(此方法为博主自己研究,问题基本解决,若有bug欢迎下方评论提出意见,我会第一时间改进代码,谢谢!) 后面其他编程题只要我写完,并成功实现,会陆续更新,记得三连哈哈! 所有答案供参考,不是标准答案,是博主自己研究的写法。(这一个题书上也有现成的代码,重要的是理解它的算法原理!)
二、题目如下:(注意:题目有一个要求(难点之一):若一个顶点有两个邻接顶点,那么下一个访问顶点的顺序要按照:A -> Z 的字典顺序访问!)
(第 2 题) 图的广度优先搜索(难度系数100)
图的广度优先搜索
描述:
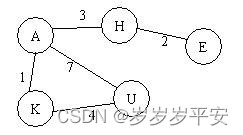
图的广度优先搜索类似于树的按层次遍历,即从某个结点开始,先访问该结点,然后访问该结点的所有邻接点,再依次访问各邻接点的邻接点。如此进行下去,直到所有的结点都访问为止。在该题中,假定所有的结点以“A”--“Z”中的若干字符表示,且要求结点的访问顺序要求根据由“A”至“Z”的字典顺序进行访问。例如有如下图:
如果要求从H开始进行广度优先搜索,则搜索结果为:H->A->E->K->U.
输入:
输入只包含一个测试用例,第一行为一个自然数n,表示顶点的个数,第二行为n个大写字母构成的字符串,表示顶点,接下来是为一个n*n大小的矩阵,表示图的邻接关系。数字为0表示不邻接,否则为相应的边的长度。
最后一行为一个字符,表示要求进行广度优先搜索的起始顶点。
输出:
用一行输出广度优先搜索结果,起始点为给定的顶点,各顶点之间用一个空格隔开。要求同一顶点的邻接点的访问顺序按“A”---“Z”的字典顺序。
样例输入:
5
HUEAK
0 0 2 3 0
0 0 0 7 4
2 0 0 0 0
3 7 0 0 1
0 4 0 1 0
H
样例输出:
H A E K U
三、代码实现:(代码的做题原理全部在代码注释中,若还有疑问也可以翻书)
补充:这里我用到的就是队列去实现广度优先算法,因为队列先进先出,先进队列的先访问,然后再相邻的顶点后进去后访问,依次下来就实现成功!
(1)我创建了最基本的图类,里面有它的很多成员变量与成员的操作方法。(所以代码会很长,但是解释了基本原理。实际上的图的广度优先遍历算法就只有一个方法在里面)
package com.fs.graph;import java.util.ArrayList;
import java.util.Collections; //用到工具类Collections
import java.util.LinkedList; //要用到LinkedListed是实现类
import java.util.Queue; //要用到队列接口,导包public class Graph_01 {//为了安全性,全部用private修饰封装,要使用或者赋值只能使用构造方法或者getter、setter方法private ArrayList<String> arrayList; //这里我用这个ArrayList集合来代替数组去存储输入的每个顶点,并设置集合里面存储的元素是String类型的private int[][] matrix; //这个二维数组:用来存储输入的矩阵,表示各个顶点相邻边的关系private int vertex; //用来表示顶点的实际个数private int maxVertex; //用来表示顶点的最大数量private boolean[] visit; //用来判断每个顶点是否被访问过public Graph_01(int vertex){this.maxVertex=10; //默认设置最大顶点个数为10this.arrayList = new ArrayList<>();this.vertex=vertex;}public ArrayList<String> getArrayList() {return arrayList;}//定位顶点的位置public int indexOfVex(String v){for(int i=0;i<vertex;i++){if(arrayList.get(i).equals(v)){return i; //找到该顶点在集合中的位置}}return -1; //否则返回-1,表示没找到该顶点}//传入包含所有顶点的字符串public void insertVer(String vertex01) throws VertexException{if(vertex01.length()>maxVertex){throw new VertexException ("超出最大顶点数!");}//存入顶点for(int i=0;i<vertex;i++){String str = vertex01.charAt(i)+"";arrayList.add(str);}}//存入顶点间边的邻接关系矩阵public void addEdge(int [][] matrix01){this.matrix=matrix01;}//实现图的广度优先搜索算法public String broadFirstSearch(int v) throws VertexException{if(v<0||v>maxVertex){//如果这个顶点不在集合中,抛出异常throw new VertexException("该顶点不存在!");}visit = new boolean[vertex]; //初始化:判断顶点是否被访问数组StringBuilder sb = new StringBuilder(); //用这个方便字符串的添加和删除,因为不会产生多余的对象,造成内存浪费,还有这个没有实现线程安全功能,效率更高//队列接口是继承Collection接口,它的实现类就有:LinkedList类Queue<Integer> queue = new LinkedList<>(); //说明里面操作时的元素类型是整型的queue.offer(v); //先把第一个访问的顶点进入队列中visit[v]=true; //并标记该顶点的访问状态为:true,表示访问过//只要队列没空就是所有的顶点还未访问完while(!queue.isEmpty()){ //判断队列是否为空v=queue.poll(); //进队列后登记完访问状态然后出队列sb.append(arrayList.get(v)+" "); //将遍历完的顶点加入字符串缓冲区ArrayList<String> arrayList01= new ArrayList<>();for(int i=vertex-1;i>=0;i--) {//邻接关系矩阵某一行中只要有不为0的值,那就是属于v顶点的这一行,还有另外有顶点与它有关系//而且要没被访问过,或者不是大于整型的最大值(表示无穷:无边的关系)if ((matrix[v][i] != 0) && (!visit[i]) && (matrix[v][i] != Integer.MAX_VALUE)) {arrayList01.add(arrayList.get(i)); //将所有满足有关系的顶点全部放在一个集合里.为了满足题目要按照字典顺序访问才这么写的}}//先把某个顶点所有的邻接顶点按照字典顺序排好序Collections.sort(arrayList01);//为了满足条件:就需要字典顺序在前的顶点先入队列,先出队先被访问。而字典顺序在后的顶点后入队列,后出队列后被访问(这样就实现了题目要求)for(int j=0;j<arrayList01.size();j++){//先从字典排序在前的顶点开始操作String str=arrayList01.get(j); //获取该顶点int index=indexOfVex(str); //再找到该顶点在之前顶点集合的位置queue.offer(index); //最后把该顶点的入队visit[indexOfVex(str)]=true; //并设置已经访问过}}//用问号表达式,如果满足前面的就输出问号后面的,否则就是输出nullreturn sb.length()>0?sb.substring(0,sb.length()):null; //用这个substring()方法,可以将StingBuilder里的字符串缓冲区里的字符串转换成String类型的}
}
//自定义异常类(考试可以不写,没做要求)
class VertexException extends Exception{public VertexException(){super();}public VertexException(String message){super(message);}
}(2)根据题目要求输入创建了测试类:
package com.fs.graph;import java.util.Scanner;public class Test_Graph_01 {public static void main(String[] args) {Scanner sc =new Scanner(System.in);int n= sc.nextInt(); //代表顶点个数String vertex = sc.next(); //代表的所有顶点的字符串Graph_01 graph = new Graph_01(n);try {graph.insertVer(vertex); //输入由各个顶点构成的字符串}catch (VertexException e){e.printStackTrace();return;}int [][] matrix01 = new int[n][n];for(int i=0;i<n;i++){for(int j=0;j<n;j++){matrix01[i][j]=sc.nextInt();}}graph.addEdge(matrix01); //传入邻接关系矩阵String v = sc.next(); //传入从某一个指定的顶点去遍历图try{String path = graph.broadFirstSearch(graph.indexOfVex(v)); //先传入起始遍历顶点,再定位其位置,最后调用广度优先算法System.out.print(path); //输出最终遍历结果}catch (VertexException e){e.printStackTrace();}}
}四、不同情况的代码测试运行结果:
<1>首先是题目中的测试输入样例:(最好手打输入测试,直接复制可能格式问题导致报错!)
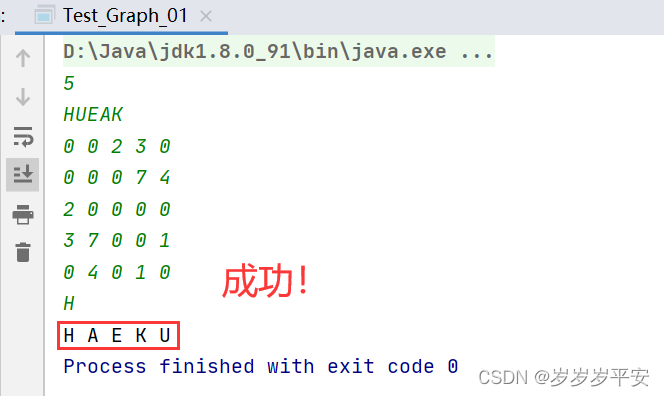
<2>自己测试的输入样例: (测试7个顶点!)
1.图展示:(手写比较随意,字有点丑哈哈!)

2.也就是测试输入样例为:
(1.)从H顶点开始遍历图:(提示最好不要直接复制我的输入样例,最好用手跟着打。因为复制完格式有点问题,就会报错)
7
HAEBKUD
0 3 2 1 0 0 0
3 0 0 0 1 7 0
2 0 0 0 0 0 0
1 0 0 0 0 0 1
0 1 0 0 0 4 0
0 7 0 0 4 0 0
0 0 0 1 0 0 0
H
代码运行后输出的遍历结果:
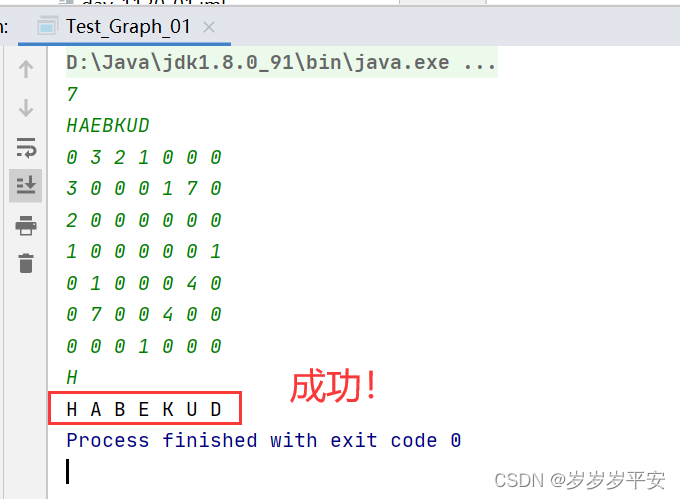
(2.)从D顶点开始遍历图:(提示最好不要直接复制我的输入样例,最好用手跟着打。因为复制完格式有点问题,就会报错)
7
HAEBKUD
0 3 2 1 0 0 0
3 0 0 0 1 7 0
2 0 0 0 0 0 0
1 0 0 0 0 0 1
0 1 0 0 0 4 0
0 7 0 0 4 0 0
0 0 0 1 0 0 0
D
代码运行后输出的遍历结果:
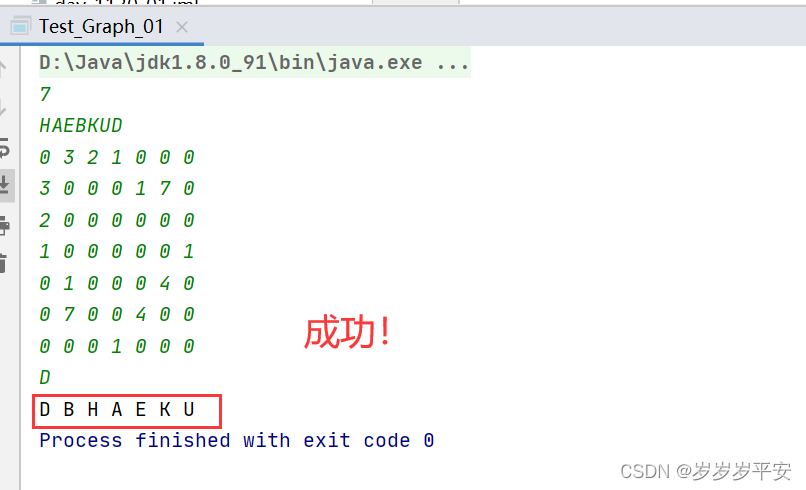

)







—————前端面试容易问到的问题总结)

)







