安装prody
pip install prody -i https://pypi.tuna.tsinghua.edu.cn/simple
eda、anm、gnm
eda(essential dynamics analysis)
另一个名字PCA(Principal Component Analysis) 或 NMA(Normal Mode Analysis)。
eda分析可以帮助人们理解生物大分子基本的运动模式和构象变化。
- 准备pdb文件
ambpdb -p com_nowat.prmtop -c com_nowat.inpcrd > amber.pdb
- 运行
prody eda namd.dcd --pdb amber.pdb --select backbone
prody eda namd_cut_450-500.dcd --pdb amber.pdb --select "calpha or nucleic and name P"
gnm(Gaussian network model)
Bahar等人在Bahar、Hinsen等人构建的残基水平上的简化模型基础上,假定各残基在平衡位置附近的运动是各向同性的高斯型运动,该模型称为高斯网络模型 (Gaussian network model, GNM)。
GNM能够计算得到不同运动模式中各个残基的运动幅度, 但是无法获得其运动的方向。
prody anm 1aar -s "calpha and chain A and resnum < 70" -A
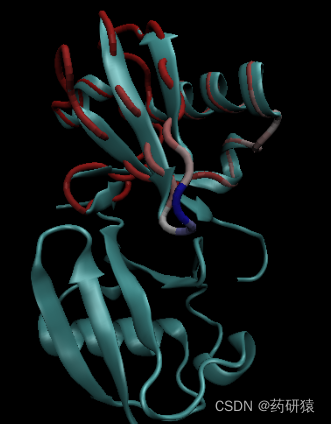
计算结果除了可以在vmd中直观地显示残基波动程度(tube粗细),还绘制了预测的b因子,相关性矩阵以及各残基波动幅度。
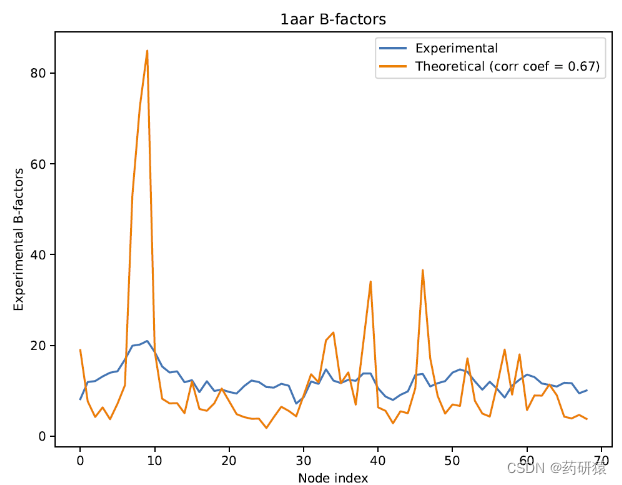
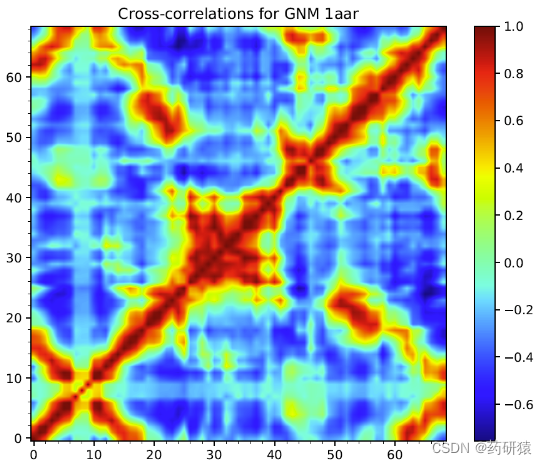
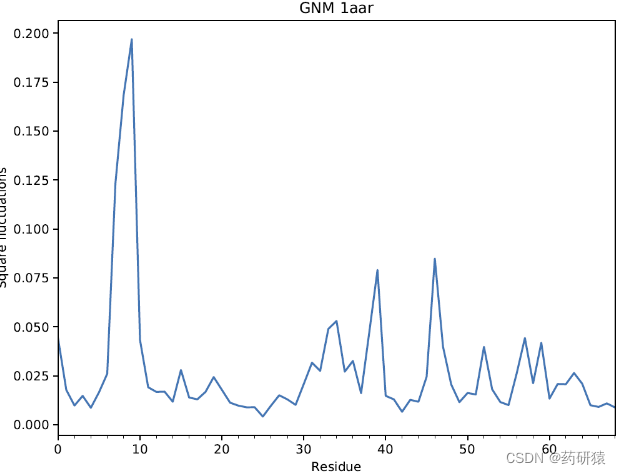
anm(anisotropic network model)
Atilgan等人将GNM进行了扩展, 考虑了残基运动的方向性信息, 将各向同性模型发展为各向异性模型, 建立了各向异性网络模型 (anisotropic network model, ANM) 。
prody anm 1aar -s "calpha and chain A and resnum < 70" -A
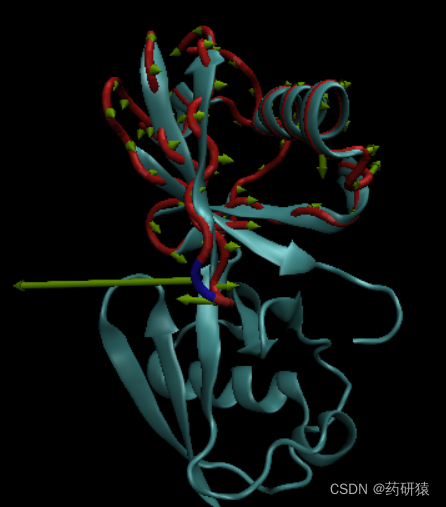
相比于gnm结果,残基上多出了箭头
后两者常用作对静态结构(晶体结构或md平衡后的某一帧)的运算,不需要输入轨迹。这样适用运算资源有限的情况。
参考博文:
ProDy学习笔记(三)—— GNM和ANM原理 - 简书 (jianshu.com)








))




:IO流)





