文章目录
- 第3章 时域分析法
- 3.1 基本概念
- 3.1.1 典型输入信号
- 3.1.2 系统动态性能指标
- 3.2 一阶系统的时间响应及动态性能
- 一阶系统的标准形式(尾1标准型)
- 3.2.1一阶惯性环节的单位阶跃响应
- 3.2.2一阶惯性环节的单位速度响应
- 3.2.3一阶惯性环节的单位脉冲响应
- 3.2.4线性定常系统时间响应的性质
- 3.3 二阶系统的时间响应及动态性能
- 二阶系统基本概念
- 临界阻尼、过阻尼系统
- 零阻尼系统
- 欠阻尼系统
- 3.4 高阶系统的时间响应及动态性能
第3章 时域分析法
- 系统分析是指对系统的稳定性、误差和动态特性三方面的性能进行分析,即分析系统的稳定性、准确性和快速性。
- 稳定性:(基本要求)系统受扰动影响后能回到原来的平衡位置;
- 准确性:(稳态要求)稳态输出与理想输出间的误差(稳态误差)要小;
- 快速性:(动态要求)阶跃响应的过程要平稳、迅速。
- 建立了控制系统的数学模型后,就可以采用不同的方法来分析和研究控制系统。本文讨论的时域分析法就是其中的重要方法之一。
- 在时间域内,上述三方面的性能都可以通过求解描述控制系统的微分方程来获得,而微分方程的解则由控制系统的结构参数、初始条件以及输入信号所决定。
- 时域分析是指在时间域内研究系统在一定输入信号的作用下,其输出信号随时间的变化情况。
3.1 基本概念
3.1.1 典型输入信号
在分析和设计控制系统时,需要有一个对各种控制系统的性能进行比较的基础,这个基础就是预先规定一些具有典型意义的实验信号作为系统的输入信号,然后比较各种控制系统对这些典型输人信号的响应,来进行分析和评价。因此,系统的时域分析就是建立在系统接受典型输入信号的基础上的。
选取典型输入信号时,必须考虑下列原则:所选输入信号应当反映系统在工作过程中的大部分实际情况;应当在形式上尽可能简单,以便于对系统响应的分析:应当能够使系统工作在最不利的情况下:应当在实际中可以得到或近似地得到,等等。
在控制工程中,通常使用的典型信号有:阶跃信号、速度信号、加速度信号、脉冲信号和正弦信号等。这些典型输入信号都是简单的时间函数,数学处理很方便,而且在实际工程中也可以实现或近似地实现,即可以进行实验研究。
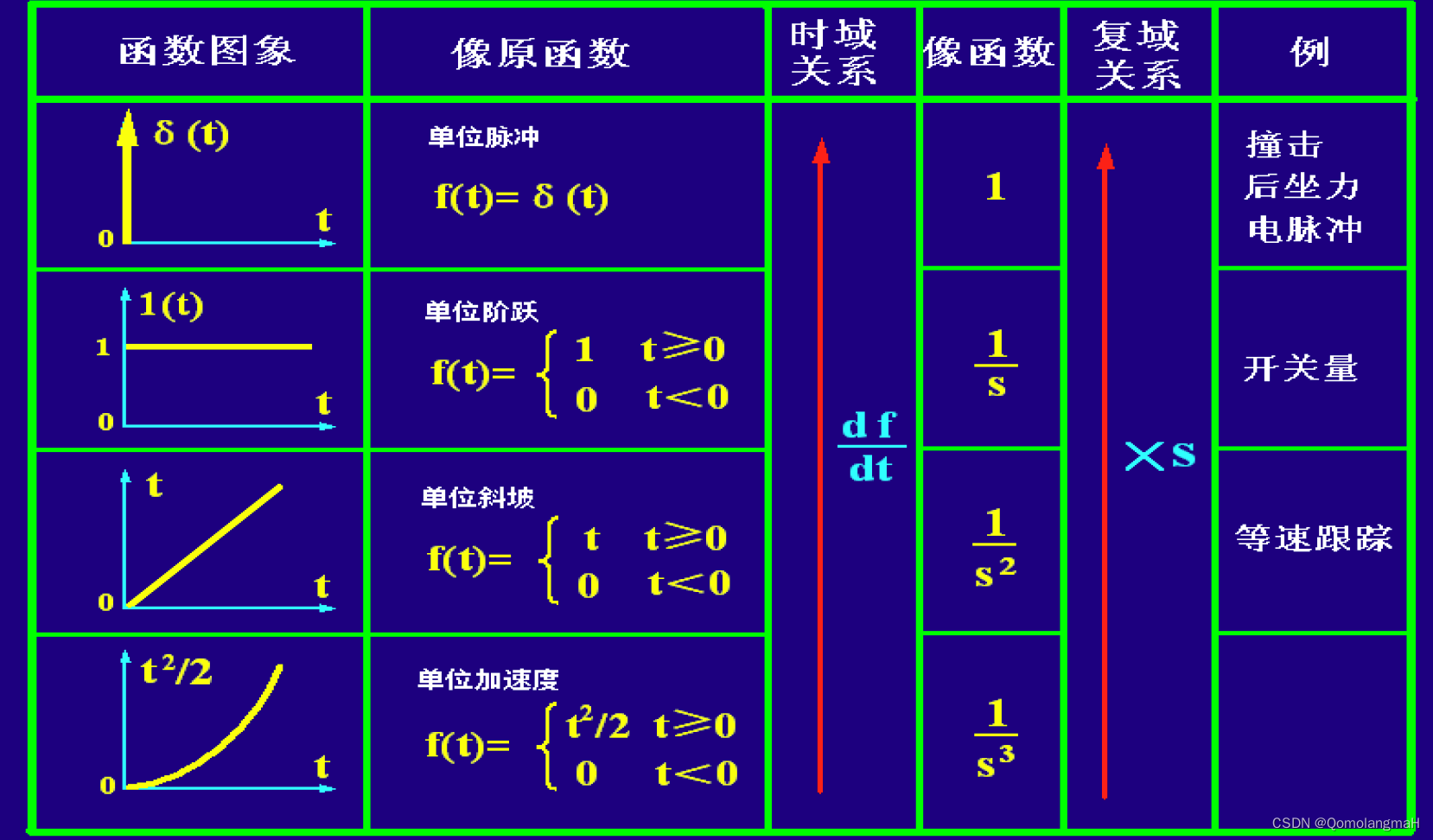
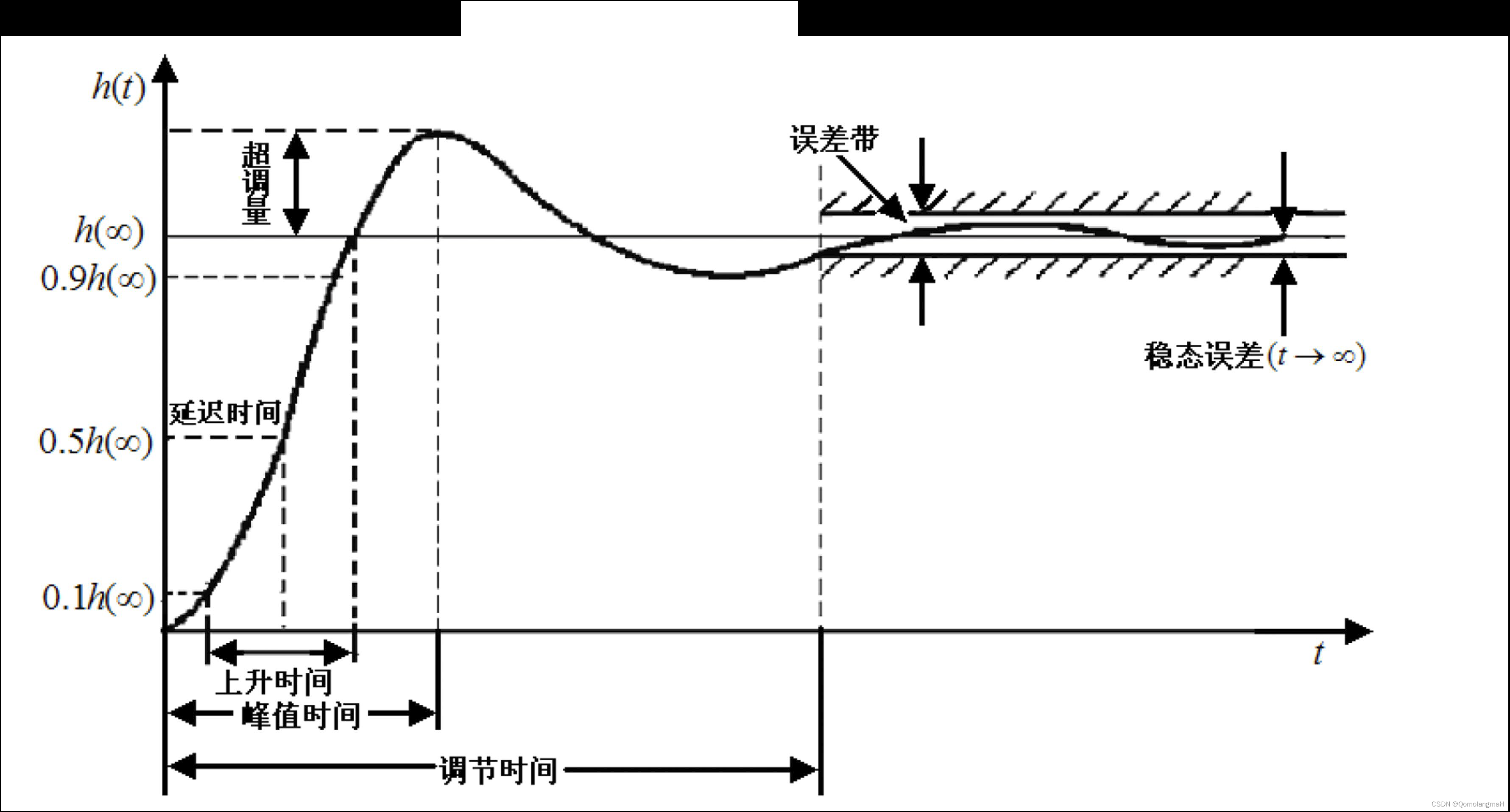
3.1.2 系统动态性能指标
- 峰值时间tp:阶跃响应越过终值达到第一个峰值所需要的时间
- 超调量𝝈%:峰值超出终值的百分比
- 调节时间𝒕𝒔:阶跃响应到达并保持在终值终值5%误差内所需要的时间
- 延迟时间 𝑡𝑑 :阶跃响应第一次达到终值的50%所需时间
- 上升时间 𝑡r
- 阶跃响应从终值10%上升到终值的90%所需的时间 (无震荡)
- 阶跃响应从0到第一次达到终值所需的时间 (有震荡)
3.2 一阶系统的时间响应及动态性能
一阶系统的标准形式(尾1标准型)

- 一阶惯性环节的单位阶跃响应
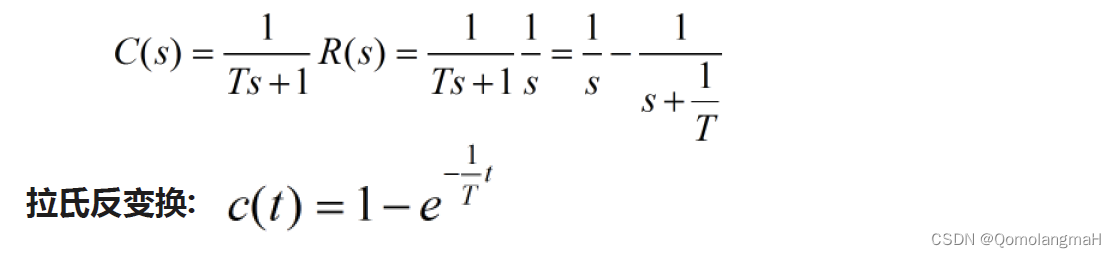
3.2.1一阶惯性环节的单位阶跃响应
- 一阶惯性环节是稳定的,无振荡
- 经过时间T,曲线上升到0.632高度,如果用实验的方法测出响应曲线达到0.632高度点时所用的时间,该时间就是一阶惯性环节的时间常数T
- 一阶系统的调节时间3T
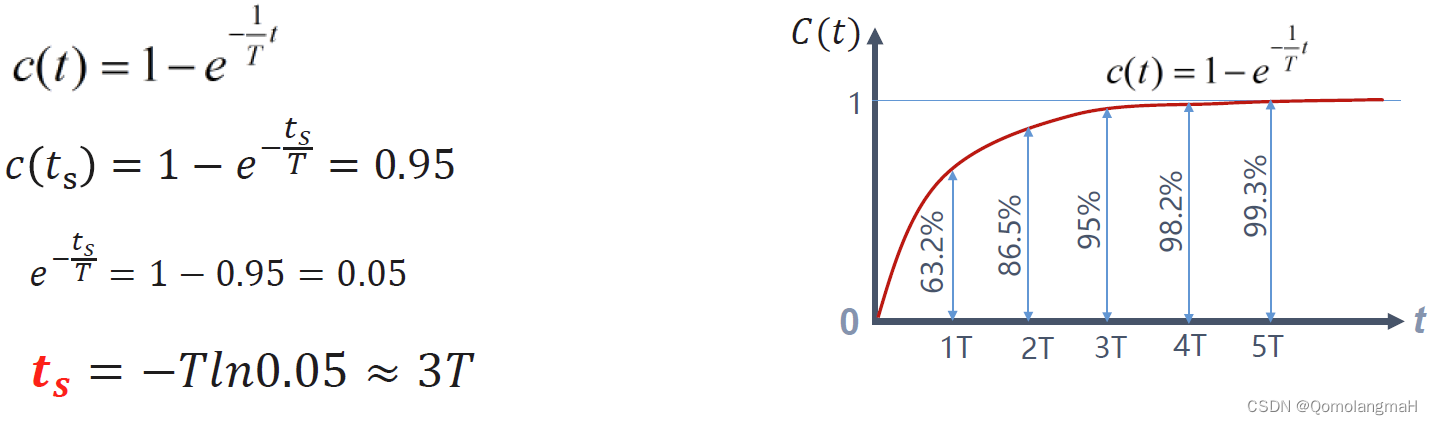
- 经过时间3T~4T,响应曲线已经达到稳态值 95%~98%,在工程上可以认为其瞬态响应过程基本结束,系统进入稳态过程
- 时间常数T 反映了一阶惯性环节的固有特性,其值越小,系统惯性越小,响应越快
3.2.2一阶惯性环节的单位速度响应
3.2.3一阶惯性环节的单位脉冲响应
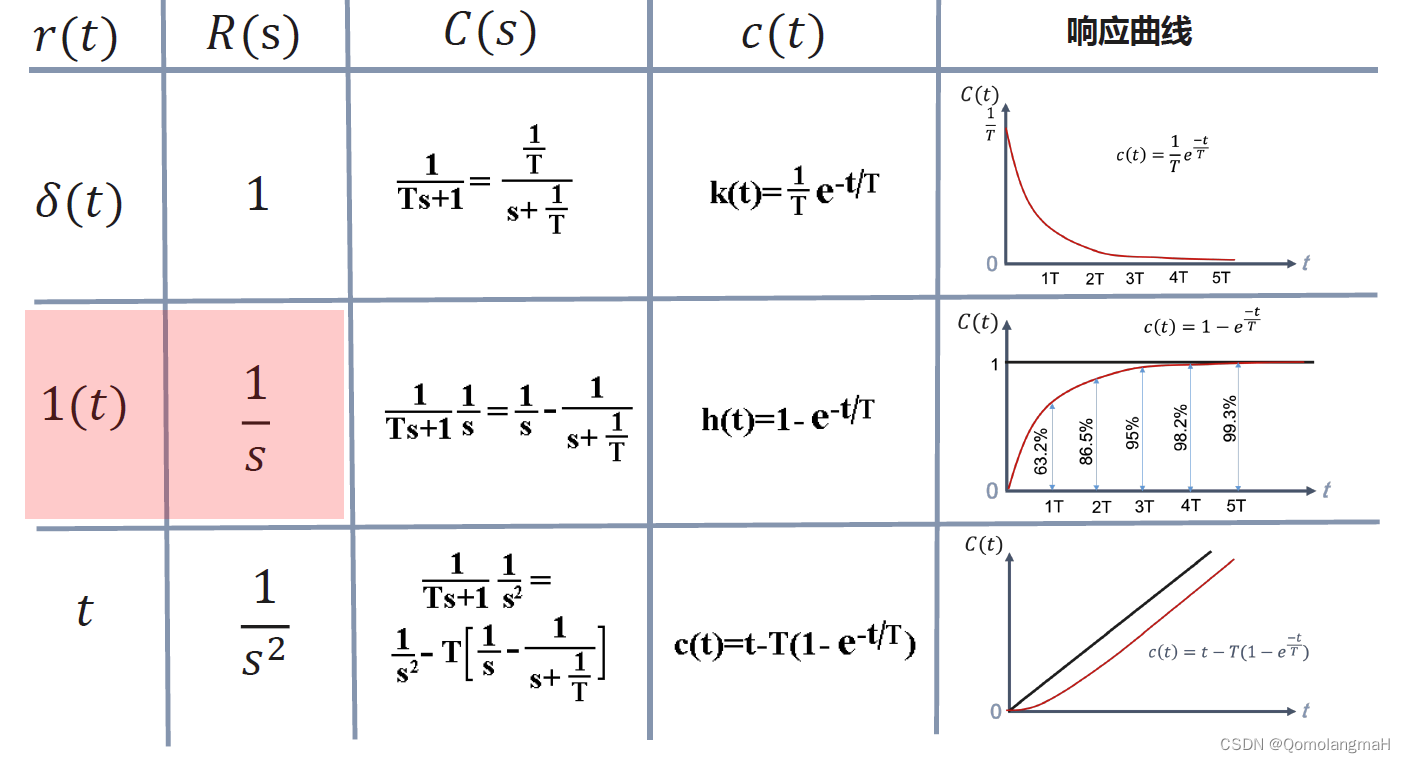
3.2.4线性定常系统时间响应的性质
单位脉冲、单位阶跃和单位速度三个典型输入信号之间存在着微分和积分的关系,而且一阶惯性环节的单位脉冲响应、单位阶跃响应和单位速度响应之间也存在着同样的微分和积分的关系。因此,系统对输入信号导数的响应,可以通过系统对该输入信号响应的导数来求得:而系统对输入信号积分的响应,可以通过系统对该输入信号响应的积分来求得,其积分常数由初始条件确定。这是线性定常系统时间响应的一个重要性质,即如果系统的输人信号存在微分和积分关系,则系统的时间响应也存在对应的微分和积分关系。
3.3 二阶系统的时间响应及动态性能
二阶系统基本概念
- 凡是能够用二阶微分方程描述的系统称为二阶系统
- 从物理上讲,二阶系统包含两个独立的储能元件,能量在两个元件之间交换,使系统具有往复振荡的趋势,所以二阶系统也称为二阶振荡环节
- 很多实际系统都是二阶系统,高阶系统在一定条件下也可以简化为二阶系统
- 因此分析二阶系统的时间响应及其特性具有重要的实际意义
- 二阶系统的典型传递函数为
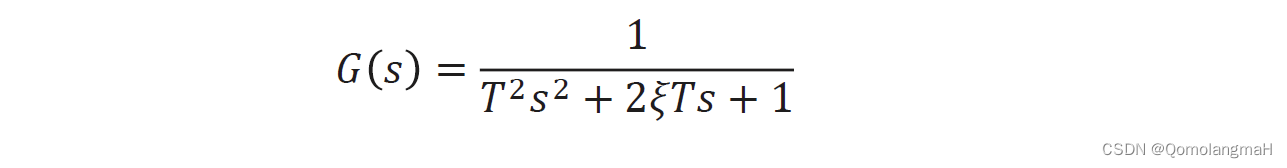
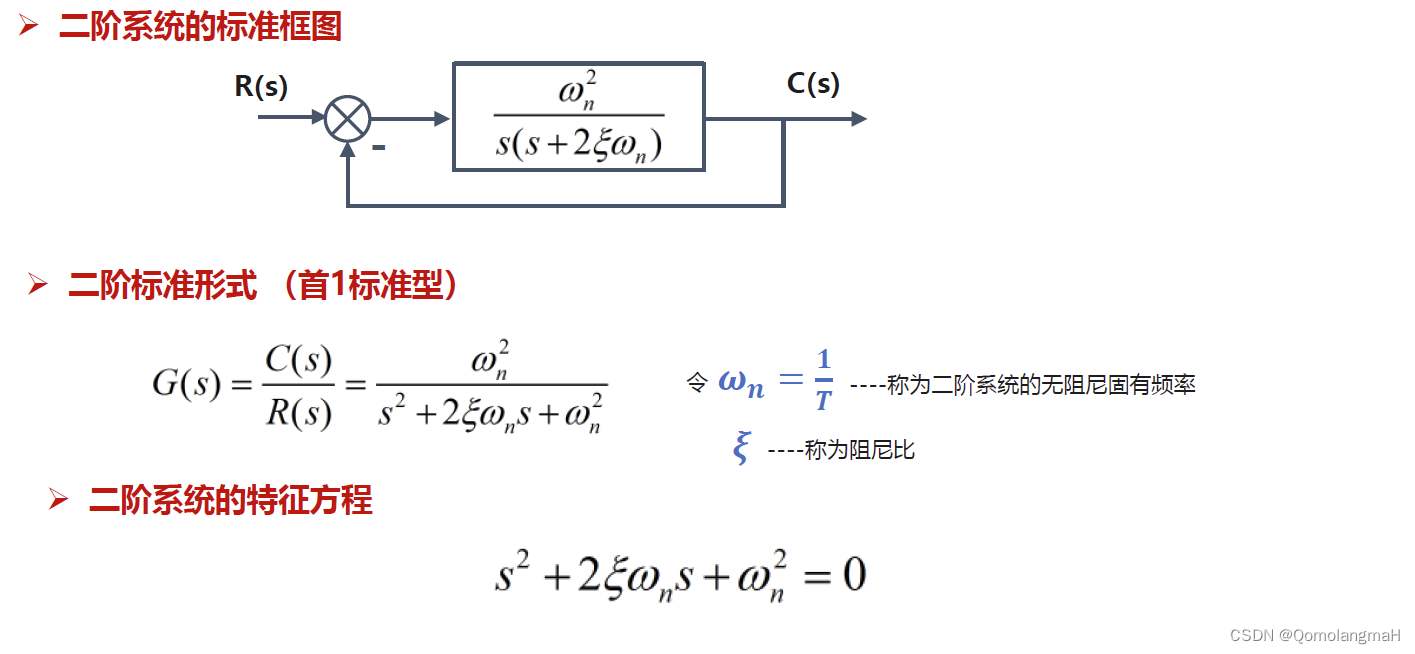
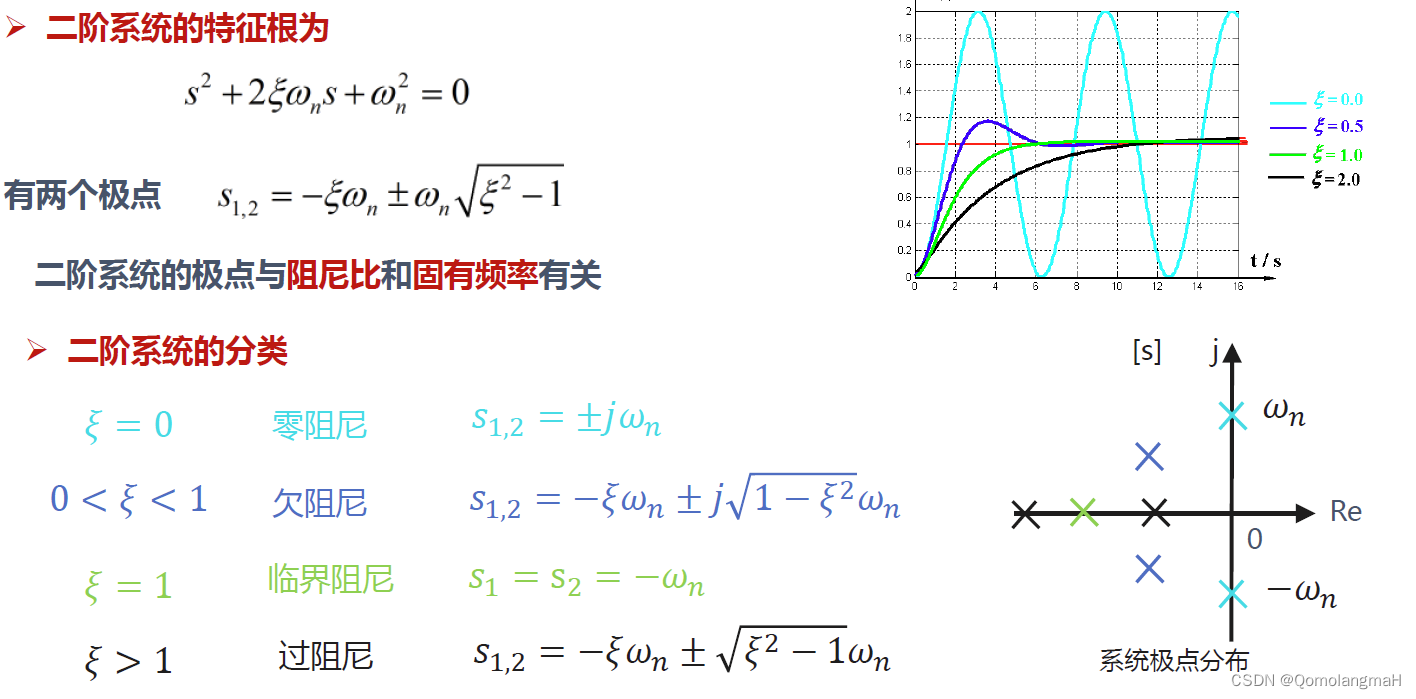
临界阻尼、过阻尼系统
零阻尼系统
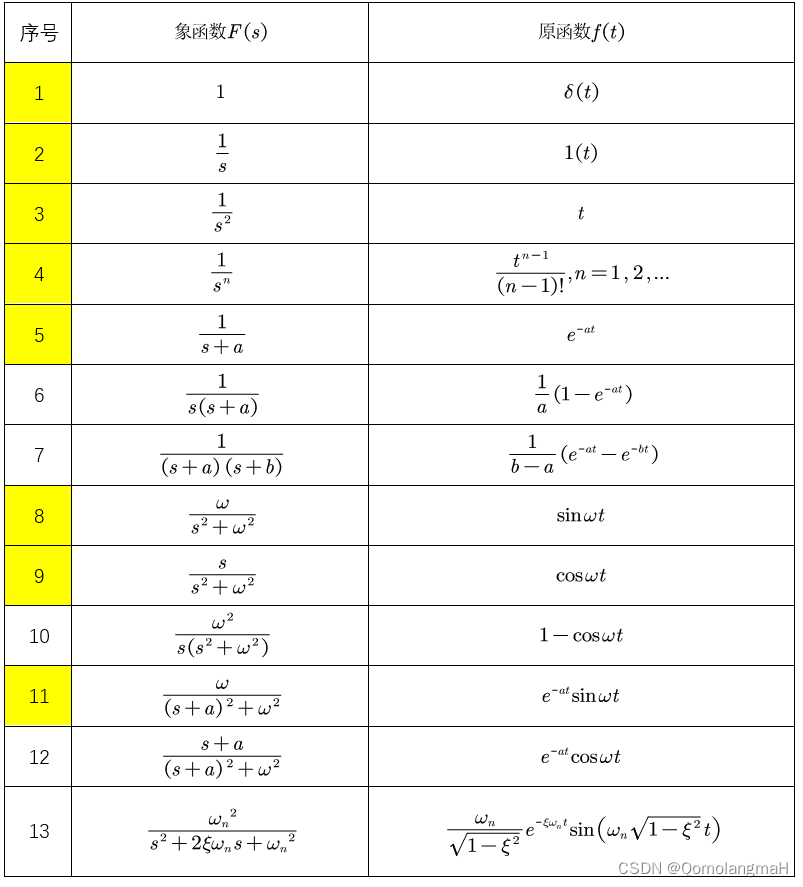
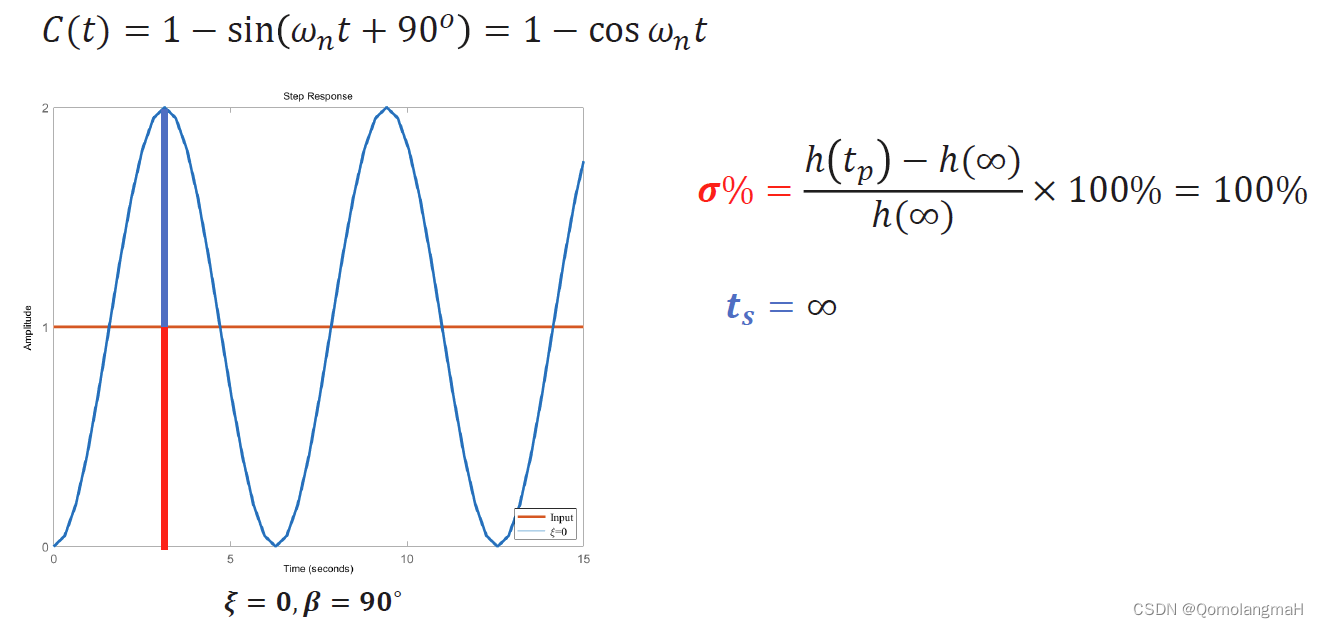
欠阻尼系统
背

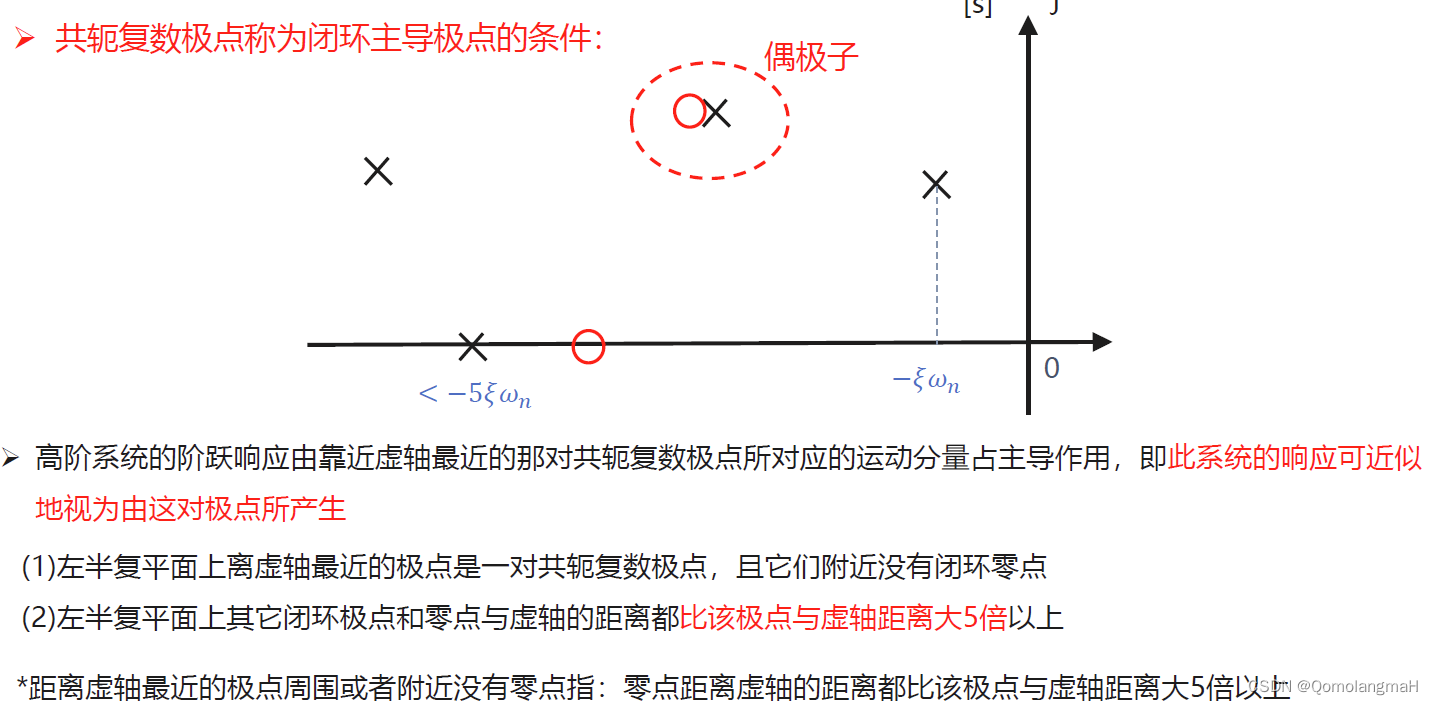
3.4 高阶系统的时间响应及动态性能
pass


-- SequenceDiagram(UML自动生成工具))


)






算法)



)

)
